а) Всего все возможных исходов: C^4_{25}C254
Всего мальчиков 25-15=10. Три юноши и одна девушка могут выиграть 4 билета Всего благоприятных событий: C^3_{10}C^1_{15}=15C^3_{10}C103C151=15C103
Вероятность того, что среди обладателей билетов окажутся 3 юноши 1 девушка равна \dfrac{15C^3_{10}}{C^4_{15}}C15415C103
б) Билеты могут получить хотя бы 1 юноша, то есть это можно рассматривать как 1 юноша и 3 девушки или 2 юноша и 2 девушки или 3 юноша и 1 девушка или 4 юноша и 0 девушек. Всего вариантов получить 4 билета может выиграть хотя бы 1 юноша Вероятность того, что среди обладателей билетов окажутся хотя бы 1 юноша равна \dfrac{10C^3_{15}+C^2_{10}C^2_{15}+15C^3_{10}+C^4_{10}C^0_{15}}{C^4_{25}}C25410C153+C102C152+15C103+C104C150
Пусть х скорость яхты, тогда скорость по течению равно х+3 км/ч а против течения х-3 км/ч. t₁=S₁/v₁=9/х+3 время по течению, время против течения равно t₂=S₂/v₂=9/х-3. Из условия t₂-t₊=2ч
получаем следующее уравнение
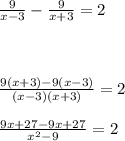
54=2(x²-9)
2x²-18=54
2x²=72
x²=36
x=±√36=±6 скорость не может быть отрицательным значением ⇒ скорость яхты 6 км/ч
ответ:6 км/ч
P.S не всегда такие задачи решаются только дискриминантом, но да частенько выходят к уравнению 2-ой степени. Главное следуй логике и условию, а проверить можно, подставив ответ в уравнение. Если мое решение понравилось отметь лучшим
1) y=3/x
гипербола в 1 и 3 чет
точки
(-3;-1)
(-2; -1,5)
(-1; -3)
(1;3)
(3;1)
y=x-2
прямая, проходящая через точки (0;-2) и (2;0)
см.рис
решение будет в точках (-1;-3) и (3;1)
2) обычное иррациональное ур-ие
возведем обе части ур-ия в квадрат
получим x^2+6x+9=4
D=16
x=-5
x=-1
ОТВЕТ: -5; -1