f(x) = 4|x| - x²
1. D(f) = R - симметрична относительно 0.
2. f(-x) = 4|-x| - (-x)² = 4|x| - x² = = f(x),
по определению f(x) - чётнвя.
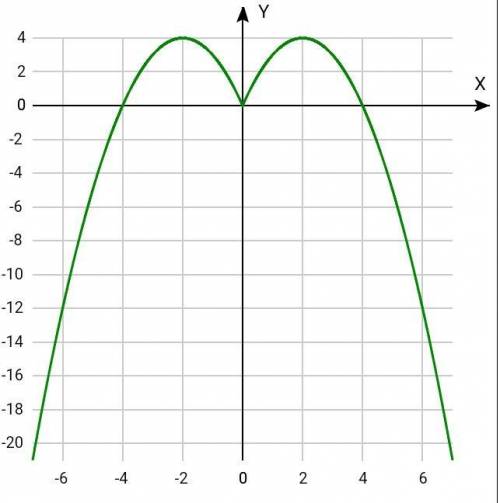
График чётной функции симметричен относительно оси Оу.
3. Построим часть графика для х ≥ 0, а затем отобразим построенную часть симметрично относительно оси Оу.
f(x) = 4x - x² - квадратичная, графиком является парабола, ветви направлены вниз, т.к. а = - 1, а<0.
х вершины = - b/(2a) = -4/(-2) = 2;
у вершины = 4•2 - 2² = 4;
(2;4) - вершина параболы.
Найдём нули функции:
4x - x² = 0
- х (х - 4) = 0
х = 0 или х = 4
(0;0) и (4;0) - точки пересечения с осью Ох.
Изображение графика смотрите в прикреплённом чертеже.
Время первой части пути будет 12/х, второй части 24/х+3. Там нужно будет поставить фигурную скобку, т.к. на весь путь он потратил 3 часа.
Расстояние первой части 12, второй 24.
Составим уравнение:
12/х+24/х+3=3. Дальше ищем общий знаменатель, т.е. х(х+3). Пишем ОДЗ: х(х+3) не равен 0
х не равен 0 и х+3 не равен 0
х не равен -3.
Получаем уравнение:
12х+36+24х=3х^2 + 9х
36х+36=3х^2 + 9х
3х^2-27х-36. Это нужно все поделить на 3
получаем: х^2 - 9х+12. Дальше решаем