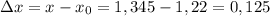
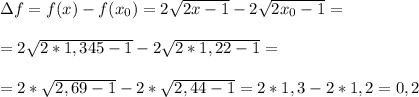
1-й
Пусть двухместных номеров х, тогда трехместных - (16 - х), в них разместились соответственно 2х и 3(16 - х) туристов. Т.к. туристов всего 42, то составим и решим уравнение
2х + 3(16 - х) = 42,
2х + 48 - 3х = 42,
-х = 42 - 48,
-х = -6,
х = 6.
Значит, двухместных номеров туристы заняли 6, а трехместных:
16 - 6 = 10 (ном.)
ответ: 6 номеров и 10 номеров.
2-й с системы)
Обозначим: х - количество двухместных номеров, y - количество трехместных номеров. По условию составим систему уравнений:
х + y = 16,
2x + 3y = 42.
Выразим из первого уравнения системы переменную х и подставим во второе уравнение:
x = 16 - y,
2(16 - y) + 3y = 42.
Решим получившееся уравнение:
2(16 - y) + 3y = 42,
32 - 2y + 3y = 42,
32 + у = 42,
y = 42 - 32,
у = 10.
Имеем: у = 10, тогда x = 16 - 10 = 6.
Значит, двухместных номеров туристы заняли 6, а трехместных - 10.
ответ: 6 и 10 номеров.
F(x) = 2*√(2*x-1)
Xo = 1.22
X1 = 1.345
НАЙТИ
ΔF/ΔX = ? - приращение функции
РЕШЕНИЕ
ΔX = X1 - Xo = 1.345 - 1.22 = 0.125 - приращение аргумента.
ΔF = F(X1) - F(Xo) - приращение функции.
Вычисляем функцию:
F(1.345) = 2*√(2.69-1) = 2√1.69 = 2*1.3 = 2.6
F(1.22) = 2*√(2.44-1) = 2√1.44 = 2*1.2 = 2.4
ΔF = 2.6 - 2.4 = 0.2 - приращение функции - ОТВЕТ
Дополнительно:
Интерес в математике представляет не само приращение функции, а скорость его изменения - дифференциал.
Отношение ΔF(x)/ΔX ≈ dF(x)/dX = F'(x) - это приблизительное значение производной в этой точке.
В задаче мы получили отношение
ΔF(x)/ΔX = 0,2/0,125 = 1,6 - приблизительное значение дифференциала.
F'(x) = 2/√(2*x-1) =
F'(1.22) = 2/1.2 = 1 2/3 ≈ 1.67 - точное значение.
График функции и касательной в точке Хо = 1,2 - на рисунке в приложении.
Но это совсем другая задача.