Вравнобедренном треугольнике основание 0,8 дм больше боковой стороны.найдите стороны треугольника,если его периметр равен 5,9

👇

Ответ:

Lilu700

09.02.2023

Пусть боковые стороны =хдм, тогда основание=х+0,8; периметр=х+х+х+0,8=5,9; 3х=5,9-0,8;3х=5,1; х=5,1:3; х=1,7 ответ: боковые стороны=1,7дм; основание=1,7+о,8=2,5дм

4,8(86 оценок)

Открыть все ответы

Ответ:

Morozob

09.02.2023

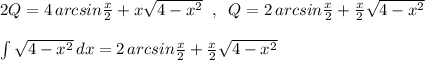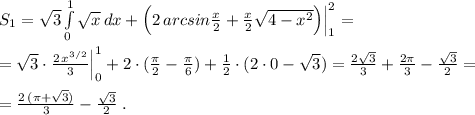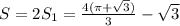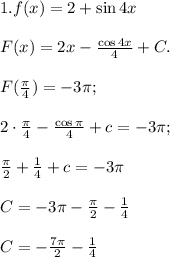
$1. f(x)=2+\sin 4x\\\\F(x)=2x-\frac{\cos4x}{4}+C.\\\\F(\frac{\pi}{4})=-3\pi;\\\\ 2\cdot\frac{\pi}{4}-\frac{\cos\pi}{4}+c=-3\pi;\\\\\frac{\pi}{2}+\frac{1}{4}+c=-3\pi \\\\ C=-3\pi-\frac{\pi}{2}-\frac{1}{4}\\\\C=-\frac{7\pi}{2}-\frac{1}{4}$

Заданная первообразная - 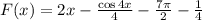$F(x)=2x-\frac{\cos4x}{4}-\frac{7\pi}{2}-\frac{1}{4}$

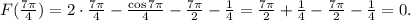
$F(\frac{7\pi}{4})=2\cdot\frac{7\pi}{4}-\frac{\cos7\pi}{4}-\frac{7\pi}{2}-\frac{1}{4}=\frac{7\pi}{2}+\frac{1}{4}-\frac{7\pi}{2}-\frac{1}{4}=0.$

ОТВЕТ: 0.

$2. f(x)=e^x+2x+1, \max_{[0;2]}F(x)=e^2.\\\\F(x)=e^x+x^2+x+C.$

График данной первообразная вне зависимости от значения константы на заданном отрезке монотонно возрастает. Поэтому максимальное значение первообразная принимает на правом конце отрезка [0; 2] - т.е. при х = 2.

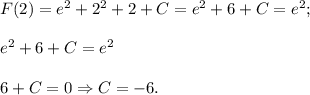
$F(2)=e^2+2^2+2+C=e^2+6+C=e^2;\\\\e^2+6+C=e^2\\\\6+C=0\Rightarrow C=-6.$

Заданная первообразная - 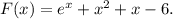F(x)=e^x+x^2+x-6.

Соответственно все из того же факта монотонного возрастания следует и то, что минимальное значение первообразная принимает на левом конце отрезка [0; 2] - т.е. при х = 0.

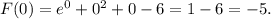
F(0)=e^0+0^2+0-6=1-6=-5.

ОТВЕТ: -5.

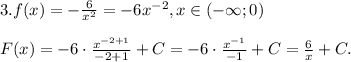
$3. f(x)=-\frac{6}{x^2}=-6x^{-2}, x\in(-\infty; 0) \\\\F(x)=-6\cdot\frac{x^{-2+1}}{-2+1}+C=-6\cdot\frac{x^{-1}}{-1}+C=\frac{6}{x}+C.$

По условию 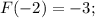F(-2)=-3;

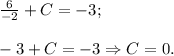
$\frac{6}{-2}+C=-3;\\\\ -3+C=-3\Rightarrow C=0.$

Заданная первообразная - 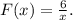$F(x)=\frac{6}{x}.$

Решим уравнение 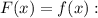F(x)=f(x):

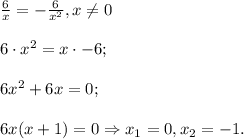
$\frac{6}{x}=-\frac{6}{x^2}, x\neq 0 \\\\ 6\cdot x^2=x\cdot-6;\\\\6x^2+6x=0;\\\\6x(x+1)=0\Rightarrow x_1=0, x_2=-1.$

Однако вспоминаем про ограничение для самой переменной: 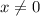$x\neq 0$ (о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение x=-1

ОТВЕТ: {-1}.

4,6(36 оценок)

Ответ:

кексик7771

09.02.2023

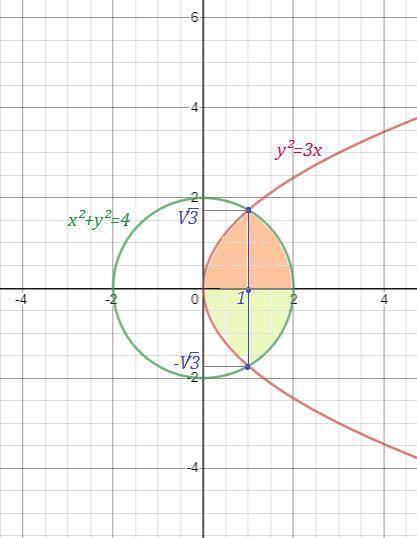
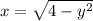$x=\sqrt{4-y^2}$ - это правая полуокружность от окружности 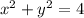x^2+y^2=4 с центром в точке (0,0) и R=2 , выразим 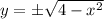$y=\pm \sqrt{4-x^2}$ , причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) .

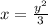$x=\frac{y^2}{3}$ - это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y: 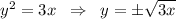$y^2=3x\; \; \Rightarrow \; \; y=\pm \sqrt{3x}$ , причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.

Область симметричная относительно оси ОХ. Поэтому можно подсчитать площадь одной половины, а затем удвоить её.

Найдём точки пересечения окружности и параболы.

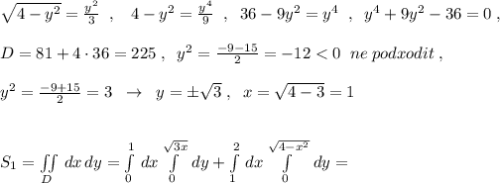
$\sqrt{4-y^2}=\frac{y^2}{3}\; \; ,\; \; \; 4-y^2=\frac{y^4}{9}\; \; ,\; \; 36-9y^2=y^4\; \; ,\; \; y^4+9y^2-36=0\; ,\\\\D=81+4\cdot 36=225\; ,\; \; y^2=\frac{-9-15}{2}=-12$

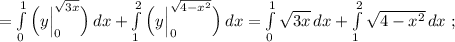
$=\int\limits^1_0\Big (y\Big |_0^{\sqrt{3x}}\Big)\, dx+\int \limits _1^2\Big (y\Big |_0^{\sqrt{4-x^2}}\Big)\, dx=\int\limits^1_0\sqrt{3x}\, dx+\int\limits^2_1\sqrt{4-x^2}\, dx\; ;$

$Q=\int \sqrt{4-x^2}\, dx\\\\Q=\int \frac{4-x^2}{\sqrt{4-x^2}}\, dx=4\int \frac{dx}{\sqrt{4-x^2}}-\int \frac{x\, \cdot \, x\, dx}{\sqrt{4-x^2}}=\Big[\; u=x\; ,\; du=dx\; ,\\\\dv=\frac{x\, dx}{\sqrt{4-x^2}}\; ,\; v=-\frac{1}{2}\cdot 2\sqrt{4-x^2}=-\sqrt{4-x^2}\; ,\; \int u\, dv=uv-\int v\, du\; \Big]=\\\\=4\cdot arcsin\frac{x}{2}-\Big(-x\sqrt{4-x^2}+\int \sqrt{4-x^2}\, dx\Big)=\\\\=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; \Rightarrow \; \; Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; ,$

$2Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}\; \; ,\; \; Q=2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}\\\\\int \sqrt{4-x^2}\, dx=2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}$

$S_1=\sqrt3\int \limits _0^1\sqrt{x}\, dx+\Big(2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}\Big)\Big|_1^2=\\\\=\sqrt3\cdot \frac{2\, x^{3/2}}{3}\Big|_0^1+2\cdot (\frac{\pi}{2}-\frac{\pi}{6})+\frac{1}{2}\cdot (2\cdot 0-\sqrt3)=\frac{2\sqrt3}{3}+\frac{2\pi }{3}-\frac{\sqrt3}{2}=\\\\=\frac{2\, (\pi +\sqrt3)}{3}-\frac{\sqrt3}{2}\; .$