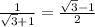
Вспомним формулу корней. У нее в знаменателе 2a. А у нас 2. Тогда хорошо бы было, если a=1.
Дальше, запишем наш корень так: 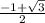 . Опять же, глядя на формулу, хорошо будет, если b=1. Теперь подберем последний коэффициент c так, чтобы дискриминант был равен числу 3. Коэффициенты a и b известны, поэтому запишем формулу дискриминанта:
. Опять же, глядя на формулу, хорошо будет, если b=1. Теперь подберем последний коэффициент c так, чтобы дискриминант был равен числу 3. Коэффициенты a и b известны, поэтому запишем формулу дискриминанта: 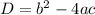
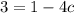
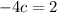
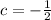
Не получилось немного.. коэффициент у нас не целый-то! Но насчет квадратного уравнения хорошо то, что если мы умножим все члены на любое отличное от нуля число, то корни не изменятся.
Из 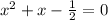 мы получаем равносильное относительно корней
мы получаем равносильное относительно корней 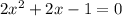
Теперь все коэффициенты целые!
С наименьшего по наибольшее раставь , средне арифметическое это сложить все числа и разделить на их количество . Допустим 1 2 3 считаем 1+2+3 получаем 6 и это число делим на 3 так как у нас 3 числа получаем 2 это средне арифметическое . Размах это от самого маленького до самого большого допустим с 2 до 5 размах равен 3 . Мода это самое повторяющееся число допустим 1 1 2 3 мода составляет 1 так как оно повторяется 2 раза . Медиана это что стоит посередине допустим 1 2 3 4 5 всего 5 цифр убираем 2 с права 2 слева остаётся 3 это медиана а если 2 числа 1 2 3 4 5 6 убираем 2 с права и 2 слева остаётся( 3+4)/2 получаем 7/2=3,5