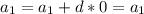проверено.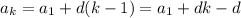
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
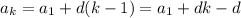то прибавив к данному выражению d. Мы получим следующий член .![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
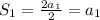. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
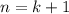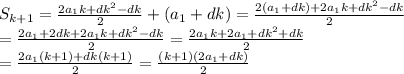
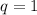получается деление на ноль, поэтому сразу пишем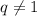 
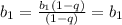
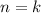
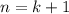:![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
1) графический метод - см. вложение
прямые пересекаются в точке с координатами (3;2), значит х = 3 y = 2
2) метод подстановки
-x+2y=4,
7x-3y=5;
х = 2y - 4,
7(2y - 4) - 3y = 5;
14y - 28 - 3y = 5
11y = 33
y = 3
x = 2*3 - 4 = 2
y = 3, x = 2
3) метод алгебраического сложения
3x-2y=64
3x+7y=-8
вычтем из 1ого уравнение 2ое :
(3x - 2y) - (3x +7y) = 64 - (-8)
-9y = 72
y = -8
Подставим полученное значение y в любое из 2х уравнений системы:
3х -2*(-8) = 64
3х = 48
х = 16
т.е. х = 16 y = -8
4) точка пересечения y=-7/8x + 17 и y = -3/5х-16:
-7/8x + 17 = -3/5х-16
7/8х - 3/5х = 33
11x/40 = 33
x = 120
y = (-7/8)*120 + 17 = -88
график уравнения y+px=0 пройдет через точку пересечения прямях (120;-88)
-88 +120p = 0
p = 88/120 = 11/15
М=а^2-3аб+5б^2.
Проверка:
в левую часть вместо М, подставляем получившиеся выражение.
а^2-3аб+5б^2-4аб+3б^2=а^2-7аб+8б^2
а^2-7аб+8б^2=а^2-7аб+8б^2, тождество выполняется.