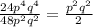
Выражение: (0.1*x^3-0.3*y)*(0.1*x^3-0.3*y)
ответ: 0.01*x^6-0.06*x^3*y+0.09*y^2
Решаем по действиям:
1. (0.1*x^3-0.3*y)*(0.1*x^3-0.3*y)=0.01*x^6-0.06*x^3*y+0.09*y^2
(0.1*x^3-0.3*y)*(0.1*x^3-0.3*y)=0.1*x^3*0.1*x^3-0.1*x^3*0.3*y-0.3*y*0.1*x^3+0.3*y*0.3*y
1.1. 0.1*0.1=0.01
X0.1
_0_._1_ _
01
0_0_ _ _
0.01
1.2. x^3*x^3=x^6
x^3*x^3=x^(3+3)
1.2.1. 3+3=6
+3
_3_
6
1.3. 0.1*0.3=0.03
X0.1
_0_._3_ _
03
0_0_ _ _
0.03
1.4. 0.3*0.1=0.03
X0.3
_0_._1_ _
03
0_0_ _ _
0.03
1.5. -0.03*x^3*y-0.03*y*x^3=-0.06*x^3*y
1.6. 0.3*0.3=0.09
X0.3
_0_._3_ _
09
0_0_ _ _
0.09
1.7. y*y=y^2
y*y=y^(1+1)
1.7.1. 1+1=2
+1
_1_
2
Решаем по шагам:
1. 0.01*x^6-0.06*x^3*y+0.09*y^2
1.1. (0.1*x^3-0.3*y)*(0.1*x^3-0.3*y)=0.01*x^6-0.06*x^3*y+0.09*y^2
(0.1*x^3-0.3*y)*(0.1*x^3-0.3*y)=0.1*x^3*0.1*x^3-0.1*x^3*0.3*y-0.3*y*0.1*x^3+0.3*y*0.3*y
1.1.1. 0.1*0.1=0.01
X0.1
_0_._1_ _
01
0_0_ _ _
0.01
1.1.2. x^3*x^3=x^6
x^3*x^3=x^(3+3)
1.1.2.1. 3+3=6
+3
_3_
6
1.1.3. 0.1*0.3=0.03
X0.1
_0_._3_ _
03
0_0_ _ _
0.03
1.1.4. 0.3*0.1=0.03
X0.3
_0_._1_ _
03
0_0_ _ _
0.03
1.1.5. -0.03*x^3*y-0.03*y*x^3=-0.06*x^3*y
1.1.6. 0.3*0.3=0.09
X0.3
_0_._3_ _
09
0_0_ _ _
0.09
1.1.7. y*y=y^2
y*y=y^(1+1)
1.1.7.1. 1+1=2
+1
_1_
2
Составляем систему уравнений с двумя неизвестными:
Y-X=7
X*Y=-12
Из верхнего уравнения выводим Y:
Y=7+Х
Подставляем Y в нижнее уравнение и получаем:
Х*(7+Х)=-12
Открываем скобки и переносим -12 в левую часть для того что бы привести уравнение к квадратному:
Х^2+7*X+12=0
Есть методика решения квадратных уравнений через дискриминант. Если дискриминант больше нуля - то квадратное уравнение имеет два решения.
Формулы нахождения решения в ссылке ниже (там же и калькулятор)
х1=-3
х2=-4
Подставляем х1 во второе уравнение:
-3*y=-12
y1=-12/-3=4
Подставляем х2 во второе уравнение:
-4*y=-12
y2=-12/-4=3