1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Пример: 5x+2y=10
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 (2)y = -2.5x+6
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5•2+6 = 1
x = 4, y = -2.5•4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y Z k0
Утверждение 1.
Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно Утверждение 2.
Если m и n уравнения (1) взаимно числа, то это уравнение имеет по крайней мере одно решение.
Утверждение 3.
Если коэффициенты m и n уравнения (1) являются взаимно числами, то это уравнение имеет бесконечно много решений:
где (; ) – какое-либо решение уравнения (1), t Z
Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
m, n, x, y Z
Утверждение 4.
Если m и n – взаимно числа, то всякое решение уравнения (2) имеет вид
5) Домашнее задание. Решить уравнение в целых числах:
9x – 18y = 5
x + y= xy
Несколько детей собирали яблоки. Каждый мальчик собрал по 21 кг, а девочка по 15 кг. Всего они собрали 174 кг. Сколько мальчиков и сколько девочек собирали яблоки?
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
1) 9x – 18y = 5
НОД (9;18)=9
5 не делится нацело на 9, в целых числах решений нет.
2) x + y= xy
Методом подбора можно найти решение
ответ: (0;0), (2;2)
1) а) (a - 4)(a - 2) = a^2 - 6a + 8
б) (3x + 1)(5x - 6) = 15x^2 - 13x - 6
в) (3y - 2c)(y + 6c) = 3y^2 + 16cy - 12c^2
г) (b + 3)(b^2 + 2b - 2) = b^3 + 5b^2 + 4b - 6
2) а) 2x(a - b) + a(a - b) = (a - b)(2x + a)
б) 3x + 3y + bx + by = 3(x + y) + b(x + y) = (x + y)(3 + b)
3) 0,2y(5y^2 - 1)(2y^2 + 1) = (y^3 - 0,2y)(2y^2 + 1) =
= 2y^5 - 0,4y^3 + y^3 - 0,2y = 2y^5 + 0,6y^3 - 0,2y
4) а) 3x - xy - 3y + y^2 = x(3 - y) - y(3 - y) = (3 - y)(x - y)
б) ax - ay + cy - cx - x + y = a(x - y) - c(x - y) - (x - y) = (x - y)(a - c - 1)
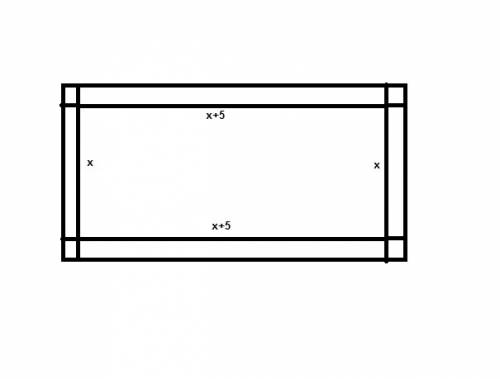
5) Размеры клумбы: x и x+5 м.
Площадь дорожки 26 кв.м., а ширина 1 м. Дорожка показана на рис.
2x + 2(x+5) + 4 = 26
x + x + 5 + 2 = 13
2x = 13 - 7 = 6
x = 3 м - ширина клумбы.
x + 5 = 3 = 5 = 8 м - длина клумбы.