y=x²-4x+3
y=ax²+bx+c
a=1, b=-4, c=3
1) Координаты вершины параболы:
х(в)= -b/2a = -(-4)/(2*1)=4/2=2
у(в) = 2²-4*2+3=4-8+3=-1
V(2; -1) - вершина параболы
2) Ось симметрии параболы проходит через вершину параболы параллельно оси Оу, значит, ось симметрии можно задать уравнением х=2
3) Точки пересечения графика функции с осями координат:
с осью Оу: х=0, y(0)=0²-4*0+3=3
Значит, (0;3) - точка пересечения параболы с осью Оу
с осью Ох: у=0, x²-4x+3=0
D=(-4)²-4*3*1=16-12=4=2²
x₁=(4+2)/2=6/2=3
x₂=(4-2)/2=2/2=1
(3;0) и (1;0) - точки пересечения с осью Ох
4) Строим график функции:
Уже найдены вершина параболы и точки пересечения с осями координат. Точка (4;3) - расположена симметрично точке (0;3) относительно оси симметрии параболы
5) По рисунку видно, что график функции находится в I, II и IV четвертях.
Объяснение:
сделай лучше ответ
1. Чтобы записать уравнение окружности, не хватает радиуса.
Стоит отметить, что расстояние от центра окружности до прямой x=3 равно радиусу, так как окружность касается этой прямой.
Центр имеет абсциссу, равную -1, а прямая -- равную 3
Найдём расстояние между -1 и 3:
R = |-1| + |3| = 1 + 3 = 4 -- радиус окружности
Теперь запишем уравнение окружности:
(x - x₀)² + (y - y₀)² = R², где (x₀, y₀) -- координаты центра окружности, R -- её радиус
(x + 1)² + (y - 5) = 16
2. Чтобы функция была чётная, нужно выполнение равенства:
y(x) = y(-x)
y(x) = xⁿ * xⁿ⁻² - 4
y(-x) = (-x)ⁿ * (-x)ⁿ⁻² - 4 = (-1 * x)ⁿ * (-1 * x)ⁿ⁻² - 4 = (-1)ⁿ * xⁿ * (-1)ⁿ⁻² * xⁿ⁻² - 4 = (-1)ⁿ⁺ⁿ⁻² * xⁿ * xⁿ⁻² - 4 = (-1)²⁽ⁿ⁻¹⁾ * xⁿ * xⁿ⁻² - 4 = 1ⁿ⁻¹ * xⁿ * xⁿ⁻² - 4 = xⁿ * xⁿ⁻² - 4
Итого y(x) = y(-x), следовательно функция чётная
3. Сначала отдельно рассмотрим первый корень. Рассмотрим подкоренное выражение, соберём из него квадрат суммы (a+b)² = a² + 2ab + b²:
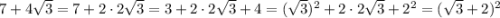
Тогда выражение примет вид:
![\sqrt[10]{7+4\sqrt{3}} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[10]{(\sqrt{3}+2)^2} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[5]{\sqrt{3}+2} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[5]{(\sqrt{3}+2)(\sqrt{3}-2)} =\sqrt[5]{(3-4)}=\sqrt[5]{-1}=-1](/tpl/images/0970/8390/45093.png)