(1-√2)² = 1 + 2 - 2*1*√2 = 3 - 2√2 ≈ 3 - 2*1,41 = 3 - 2,82 = 0,18 ∈ [0; 0,5)
ответ: Б).
Если не верите, то вот более строгое доказательство:
Предположим, вариант Б) верный. Тогда (1-√2)² должно быть меньше, чем 0,5, а также больше либо равно, чем 0. Проверим оба эти условия. Итак, сравним (1-√2)² и 0. Т.к. √2 > 1 (т.к. (√2)² = 2 > 1 = 1²), то число 1 - √2 точно не равно нулю, а значит, его квадрат точно больше нуля. Доказали. Теперь осталось доказать, что (1-√2)² меньше, чем 0,5, или что 3 - 2√2 меньше, чем 0,5, то есть:
3 - 2√2 < 0.5 ?
-2√2 < 0.5 - 3 ?
-2√2 < -2.5 ?
2√2 > 2.5 ?
√2 > 1.25 ?
Т.к. (√2)² = 2 > 1.5625 = (1,25)², то и √2 > 1.25, а значит исходное выражение ((1-√2)² < 0.5) - верное, а значит, наше предположение, что ответ Б) - верный, оказалось правильным. Да, действительно (1-√2)² ∈ [0; 0,5)
Область определения функции: функция существует, если знаменатель дроби не обращается в нуль, т.е.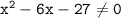
Упростим функцию: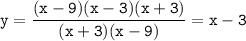
Получили линейную функцию; графиком линейной функции является прямая, проходящая через точки (0;-3), (3;0).
Графики функций не имеют общих точек, если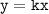
проходит через выколотые точки, т.е. через точки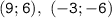 
Подставляя координаты, получим:
Решим теперь уравнение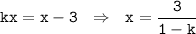
Очевидно, что при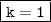
уравнение решений не имеет, а следовательно, графики функций при k=1 не имеют общих точек.
ответ: 2/3; 1; 2.