Общий вид квадратного уравнение следующее
a·x²+b·x+c=0, где a≠0.
Неполное квадратное уравнение имеет один из следующих видов:
a·x²+c=0 когда b=0; a·x²+b·x=0 когда c=0;a·x² = 0 когда b=c=0.1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:
a·x²+c=0 ⇔ a·x² = -c ⇔ x² = -c/a, так как -c/a>0 ⇔ 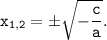
Тогда
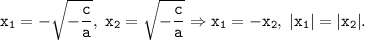
Отсюда условие:
b=0 и c/a<0!
b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:
a·x²=0 ⇔ x²=0 ⇔ x=0.
Отсюда условие:
b=c=0!
В случае a·x²+b·x=0 квадратное уравнение имеет два корня:
a·x²+b·x=0 ⇔ x·(a·x+b)=0 ⇒ x₁=0, x₂= -b/a.
13 000 рублей
Объяснение:
Костюм на 4000 р дороже, чем футболка, значит 4 костюма стоят как 4 футболки плюс 4×4000 = 4 футболки + 16 000
По условиям 4 костюма и 2 футболки стоят 70 000. Значит 4 футболки + 16 000 + 2 футболки = 70 000
4 футболки + 16 000 + 2 футболки = 4 футболки + 2 футболки + 16 000 = 6 футболок + 16 000
Значит 6 футболок + 16 000 = 70 000
Значит 6 футболок = 70 000- 16 000 = 54 000
Значит она футболка стоит 54 000 ÷ 6 = 9 000
А костюм на 4000 дороже - значит он стоит 9000+4000=13 000 рублей
a)f`(x)=√(x²-1)+2x(x-1)/2√(x²-1)=(x²-1+x²-x)/√(x²-1)=(2x²-x-1)/√(x²-1)
f`(2)=(8-2-1)/(√(4-1)=5/√3
b)y`=-1/√(1-(2x-1)³/3)*2/√3=-2√3/√3*√(2-4x²+4x)=-2/√(2-4x²+4x)
2
y=x³-6x²+9
D(y)=R
y(-x)=-x³-6x²+9 ни четная,ни нечетная
(0:9)-точка пересечения с осью оу
y`=3x²-12x=3x(x-4)=0
x=0 x=4
+ _ +
(0)(4)
возр x∈(-∞;0) U (4;∞)
убыв x∈(0;4)
ymax=y(0)=9
ymin=y(4)=-31
доп.точки
y(-1)=2
y(1)=4
y(5)=-16
график во вложении
3
1)Sx²dx/√(x³-5)=1/3Sdt/√t=2t/3=2√(x³-5)/3+C
t=x³-5⇒dt=3x²dx
2)S(4-3x)*e^3xdx=S(4e^3x-3x*e^3x)dx=-3Se^3x*xdx+4Se^3xdx=
=-e^3x*x+e^3x/3+4e^3x/3=-e^3x*x+5e^3x/3=e^3x(5/3-x)+C
В 4 в условии ошибка