выражаем из первого ур-я у
получаем у=3х+12
подставляем во второе вместо у
получим
-9хквадрат+5(3х+12)квадрат+144=0
далее решаем это уравнение
возведем в квадрат выражение(3х+12) и упростим уравнение
-9хквадрат+45хквадрат+360х+720+144=0
36хквадрат+360х+864=0
вынесем 36 за скобки, получим
36(хквадрат+10х+24)=0, сократим на 36 и найдем корни через дискриминант
это будет х=-10+-корень квадратный из 100-4*24
получим х=(-10+-2)/2
корни -6 и-4
теперь подставим в первое уравнение эти корни и найдем у
получим у=3(-6)-12=-30 и у=3(-4)-12=-24
ответ система имеет решения при у1=-30,у2=-24, и х1=-6 и х2=-4
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)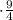 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 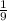 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 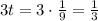 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 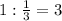 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.

1)x=6, y=-6
2) x=4, y=0