Question

Найдите область определения функции а) y=√5x-4x^2 (всё выражение под квадрат. корнем) б) y=√x^2+2x-80 (под квадрат. корнем) /3x-36

Answer 1

а) x∈[0; 1,25]

б) x∈(-∞; -10]∪[8; 12)∪(12; +∞)

Объяснение:

а)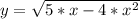 $y=\sqrt{5*x-4*x^{2} }$

Область определения функции:

подкоренное выражение должен быть неотрицательным

5·x-4·x²≥0

x·(5-4·x)≥0

Нули левой части неравенства

х=0 и 5-4·x=0 или х=0 и x=5/4=1,25

Применим метод интервалов

x·(5-4·x):                   -                           +                                    -

       -∞      ----------- -1 -----------[0]------- 1 ----------[1,25]---------- 100 --------------> +∞

То есть  

при х= -1 : -1·(5-4·(-1)) = -1·(5+4) = -1·9 = -9<0

при х= 1 : 1·(5-4·1) = 1·(5-4) = 1·1 =1>0

при х= 100 : 100·(5-4·100)) = 100·(5-400) = 100·(-395) =-39500<0

ответ: x∈[0; 1,25]

б)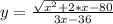 $y=\frac{\sqrt{x^{2} +2*x-80}}{3x-36}$

Область определения функции:

1) подкоренное выражение должен быть неотрицательным

x² + 2·x - 80≥0

Левую часть разложим на множители, для этого решаем как квадратное уравнение

D= 2²-4·1·(-80)=4+320=324=18²

x₁=(-2-18)/2= -20/2 = -10

x₂=(-2+18)/2= 16/2 = 8

(x - (-10))·(x-8)≥0

Нули левой части неравенства - это корни квадратного уравнения.

Применим метод интервалов

(x+10)·(x-8):      +                                -                                +

  -∞ ----------- -100 -----------[-10]------- 0 ----------[8]---------- 100 -------------> +∞

То есть  

при х= -100: (-100+10)·(-100-8)) = -90·(-108) = 90·108 >0

при х= 0 : (0+10)·(-8)) = 10·(-8) = -80 <0

при х= 100 : (100+10)·(100-8)) = 110·92 >0

ответ: x∈(-∞; -10]∪[8; +∞)

2) знаменатель не должен быть нулем

$\left \{ {{x^{2} +2*x-80\geq 0} \atop {3*x-36 \neq 0}} \right.$

3·x-36≠0 или 3·x≠36 или x≠12.

Тогда ответ: x∈(-∞; -10]∪[8; 12)∪(12; +∞)

Answer 2

a) D(y) = [0; 1.25]

б) D(y) = (-∞; -10] U [8; 12) U (12; +∞).

Объяснение:

а) у = √(5х - 4х²)

Подкоренное выражение не должно быть отрицательным, поэтому

5х - 4х² ≥ 0

Найдём корни уравнения 5х - 4х² = 0

х(5 - 4х) = 0

х1 = 0;   х2 = 1,25

Делим на интервалы и определяем знаки на интервалах. Получаем следующую картинку

   -                      +                     -

0 1,25

Очевидно, что 5х - 4х² ≥ 0 при х∈[0; 1.25], поэтому область определения функции D(y) = [0; 1.25].

б)  y = (√(x² + 2x - 80))/(3х - 36)

Знаменатель функции не должен быть равен нулю, поэтому

3х - 36  ≠ 0  ⇒ х ≠ 12

Подкоренное выражение не должно быть отрицательным, поэтому

x² + 2x - 80 ≥ 0

Найдём корни уравнения x² + 2x - 80 = 0

D = 4 + 320 = 324

х1 = 0,5(-2 - 18) = -10

х2 = 0,5(-2 + 18) = 8

Делим на интервалы и определяем знаки на интервалах. Получаем следующую картинку

   +                      -                     +              +

-10 8 12

Очевидно, что x² + 2x - 80 ≥ 0 при х∈(-∞; -10] U [8; 12) U (12; +∞), поэтому область определения функции D(y) = (-∞; -10] U [8; 12) U (12; +∞).