1. Известно, что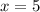 
, 
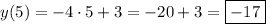
2. Известно, что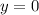 
, тогда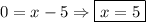 
3. Обе точки имеют координаты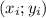 
, причем при подставлении этих координат в уравнение функции, мы получаем верное равенство.
Смотрим на точку А: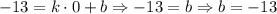 
Отлично, уравнение известно теперь в таком виде: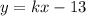 
, в него подставим вторую точку и найдем 
.
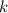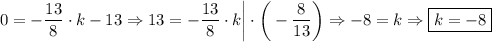
4. Решаем аналогично. Точка А: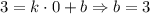 
Уравнение уже в виде: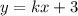 
Точка B: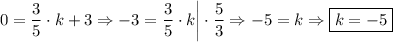 
5. Условие симметрии относительно прямой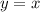 
такое, что у функции 
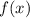меняются местами область определения и область значений, то есть подставляя 
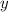вместо 
мы получаем по итогу . При взаимно однозначном соответствии области определения и области значений (как в случае прямых) все вообще просто и работает везде.
Что нужно сделать: есть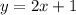 
, делаем
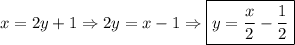
Координаты вершины параболы (-2; -16)
Объяснение:
1. Найдите координаты вершины параболы y=x²+4x-12.
Координаты вершины параболы определяются по формуле:
х₀= -b/2a= -4/2= -2
у₀= (-2)²+4*(-2)-12= 4-8-12= -16
Координаты вершины параболы (-2; -16)
2. Постройте график функции y=x²+4.
Найдите промежутки, на которых y<0
График парабола, ветви направлены вверх.
Таблица:
х -3 -2 -1 0 1 2 3
у 13 8 5 4 5 8 13
Функция не имеет отрицательных значений, так как график находится полностью выше оси Ох, координаты вершины параболы (0; 4)
2x(x-2y^2)=0
2x=0 или x-2y^2=0
x=0 x=2y^2