Question

Определить вид кривой второго порядка, построить её, найти вершины и фокусы. х^2+25y^2=25, y^2-24x=0, 2x^2-5y^2=10

Answer 1

Найдём инвариант кривой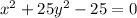 $x^{2}+25y^{2}-25=0$

Delta=$\left[\begin{array}{ccc}1&0&0\\0&25&0\\0&0&-25\end{array}\right] = 1*(25*(-25)-0)=-625\neq0$ => кривая невырожденная

$D= \left[\begin{array}{ccc}1&0\\0&25\\\end{array}\right] = 1*25=250$

$I=1+25=26$

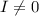Delta* $I\neq0$ => кривая центральная

$D0$ и Delta*I<0 => кривая - эллипс

Найдём инвариант кривой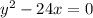 $y^{2}-24x=0$

Delta=$\left[\begin{array}{ccc}0&0&-12\\0&1&0\\-12&0&0\end{array}\right] = (-12)*(0-1(-12))=-144\neq0$ => кривая невырожденная

$D= \left[\begin{array}{ccc}0&0\\0&1\\\end{array}\right] = 0$

$I=0+1=1$

$D=0$ => кривая - парабола

Найдём инвариант кривой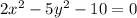 $2x^{2}-5y^{2}-10=0$

Delta=$\left[\begin{array}{ccc}2&0&0\\0&-5&0\\0&0&-10\end{array}\right] = 2*((-5)*(-10)-0)=100\neq0$ => кривая невырожденная

$D= \left[\begin{array}{ccc}2&0\\0&-5\\\end{array}\right] = 2*(-5)=-10<0$

$I=2+(-5)=-3$

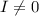Delta* $I\neq0$ => кривая центральная

$D0$ => кривая - гипербола