Ть опервый использование свойств арифметической прогрессии) Имеем конечную арифметическую прогрессию с первым членом -111, разностью арифметической прогрессии 1 (разница между двумя последовательными целыми числами) и суммой 339, нужно найти последний член данной прогрессии
- не подходит, количество членов прогрессии не может быть отрицательным ответ: 114
второй на смекалку) (так как слагаемые последовательные целые числа, и меньшее из них отрицательное, а сумма положительна, то последнее из них тоже положительное, иначе они б в сумме дали отрицательное число как сумму отрицательных числе, а не положительное)
далее -111+(-110)+.+0+1+2+...+110+111+112+...+х= (-111+111)+(-110+110)+(-99+99)+(-1+1)+0+112+113+114+.. + х= 0+0+0+....+0+0+112+113+114+..+х =112+113+..+х т.е каждому отрицательному найдется в "противовес" положительное, которое в сумме вместе с ним даст 0, и фактически наша сумма равна 112+113+...+х (*) так как наименьшее из слагаемых (*) трицифровое ,и наша сумма трицифровое число, то мы последовательно сравнивая суммы , найдем его очень быстро 112=112 112+113=225 - меньше 112+113+114=339 -- совпало значит искомое число х равно 114 ответ: 114
Решаю векторами.
Компоненты векторов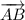 ,
, 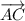 и
и 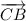 :
:
Нормы (модули, величины, длины) этих векторов:
Угол между векторами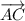 и
и 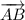 :
:
Скалярное произведение
Имеем
В градусах:
Угол между векторами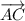 и
и 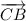 :
:
Скалярное произведение
Имеем
В градусах:
Нас интересует угол
Сумма углов будет