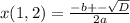
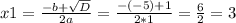
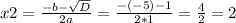
![\sqrt[3]{b^3} =b](/tpl/images/1360/0500/b0499.png) - корень нечетной степени
- корень нечетной степени
![\sqrt[6]{b^6} =|b|](/tpl/images/1360/0500/b8ca9.png) - для корней четной степени появляется модуль
- для корней четной степени появляется модуль
Неравенства сводятся к таким:  и
и 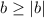
По определению модуля: 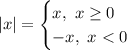
Таким образом, первое неравенство выполняется всегда. Для положительных чисел и нуля модуль равен самому числу. Для отрицательных чисел, само число меньше модуля, так как модуль будет положительным числом.

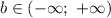
Второе неравенство выполняется при неотрицательных 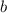 . Для положительных чисел и нуля модуль по-прежнему равен самому числу. Однако, отрицательное число не может быть больше или равно модуля, так как модуль отрицательного числа - положителен.
. Для положительных чисел и нуля модуль по-прежнему равен самому числу. Однако, отрицательное число не может быть больше или равно модуля, так как модуль отрицательного числа - положителен.
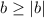
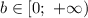
Пусть первый может набрать весь текст за х часов, второй за y часов.
Примем всю работу за 1.
Значит, первый за час выполняет 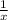 часть работы.
часть работы.
Второй за час выполняет 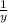 часть работы.
часть работы.
Вместе за час они выполнят: 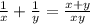
За 8 часов выполнят: 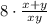 , т.е всю работу 1
, т.е всю работу 1
Первое уравнение:

Если первый оператор будет работать 3 ч,
а второй 12 ч, то они выполнят только 75%=0,75 всей работы.
Второе уравнение:
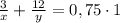
Решаем систему двух уравнений:
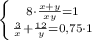

умножим первое уравнение на 3, второе уравнение на 4
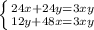
Приравниваем левые части:
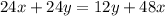
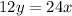
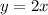
и подставляем в первое уравнение системы: 
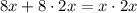 ⇒
⇒ 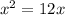 ( х=0 не удовл смыслу задачи)
( х=0 не удовл смыслу задачи)
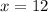
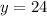
О т в е т. первый может набрать весь текст за 12 часов, второй за 24 часа.
(x-2)(x-3)(x-4)-(x-3)(x-4)(x-5)=0
Выносим за скобки (x-3)(x-4):
(x-3)(x-4)((x-2)-(x-5))=0
Это произведение будет равно нулю, если:
x-3=0 или x-4=0 или (x-2)-(x-5)=0
Следовательно:
x1=3
x2=4
(x-2)-(x-5)=0
x-2-x+5=0
3=0 - не имеет решений.
ответ: x1=3, x2=4