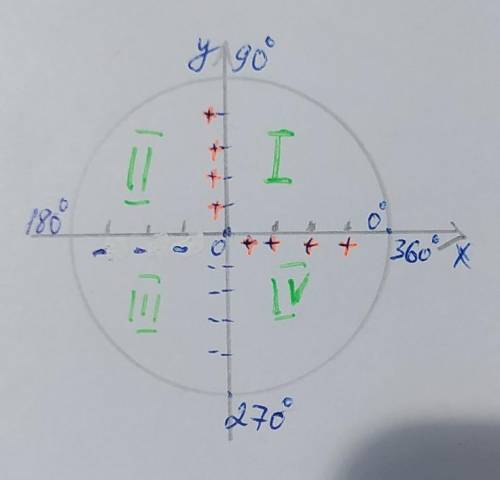
чтобы определить знак функции достаточно определить в какой координатной четверти она находится. Знаки синуса соответствуют знакам на оси у, а знаки косинуса оси х.
В)
1) –83° – угол отрицательный, приведём его к положительному:
(–83°+360°)=277°; 277° ∈ [270°; 360°] – Ⅳ четверть.
sin 277° < 0; cos 277° > 0
2) 198° ∈ [180°; 270°] – Ⅲ четверть.
sin 198° < 0; cos 198° < 0
3) –295° < 0, приведём его к положительному:
(–295°+360°)=65°; 65° ∈ [0°; 90°] – Ⅰ четверть;
sin 65° > 0; cos 65° > 0
4) 1540°=(4×360°+100°)=(1440°+100°)=100°; 100° ∈ [90°; 180°] – Ⅱ четверть;
sin 100° > 0, cos 100° < 0
Г) Для удобства переведем радианы в градусную меру.
1) π/15=180°÷15=12°; 12° ∈ [0°; 90°] – Ⅰ четверть;
sin 12° > 0; cos 12° < 0
2) –17π/14= –17×180÷14≈ –219° < 0;
(–219°+360°)=141°; 141° ∈ [90°; 180°] – Ⅱ четверть;
sin 141° > 0; cos 141° < 0
3) 40π/21=40×180÷21≈343°;
343° ∈ [270°; 360°] – Ⅳ четверть;
sin 343° < 0; cos 343° > 0
4) –37π/30= –37×180÷30= –222° < 0;
–222°+360°=138°; 138° ∈ [90°; 180°] – Ⅱ четверть;
sin 138° > 0; cos 138° < 0
В решении.
Объяснение:
1. Линейные: а); г).
2.
а) у = х -3; у = 2х - 1;
k₁ ≠ k₂, прямые пересекаются;
б) у = 5 - 2х; у = 5 - 2х;
k₁ = k₂, прямые совпадают.
3. у = 2,8х - 5; у = -1,2х + 7;
Приравнять правые части (левые равны) и вычислить х:
2,8х - 5 = -1,2х + 7
2,8х + 1,2х = 7 + 5
4х = 12
х = 12/4
х = 3;
Теперь подставить значение х в любое из двух данных уравнений и вычислить у:
у = 2,8х - 5
у = 2,8 * 3 - 5
у = 3,4;
Координаты точки пересечения прямых: (3; 3,4).
4. 4х + 5у = 9
12х + 15у = 18
Разделить второе уравнение на 3 для упрощения:
4х + 5у = 9
4х + 5у = 6
Умножить первое уравнение на -1, чтобы решить систему сложением:
-4х - 5у = -9
4х + 5у = 6
Сложить уравнения:
-4х + 4х - 5у + 5у = -9 + 6
0 = -3
Система уравнений не имеет решений.
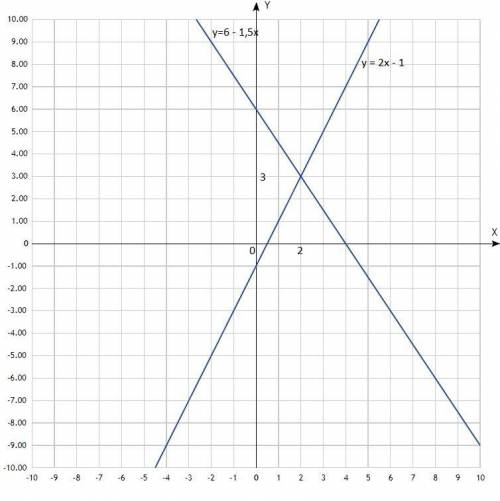
5. 3х + 2у = 12
2х - у = 1
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Прежде преобразовать уравнения в уравнения функций:
3х + 2у = 12 2х - у = 1
2у = 12 - 3х -у = 1 - 2х
у = (12 - 3х)/2 у = 2х - 1
у = 6 - 1,5х
Таблицы:
х -2 0 2 х -1 0 1
у 9 6 3 у -3 -1 1
Координаты точки пересечения прямых: (2; 3).
Решение системы уравнений: (2; 3).
Здесь применяется формула суммы кубов.