![x^{0.5*\log_3x}=\sqrt[3]x\\ \log_3x^{0.5*\log_3x}=\log_3x^\frac{1}{3}\\ 0.5*\log_3x*\log_3x=\frac{1}{3}*\log_3x\\ \frac{1}{2}*\log_3^2x-\frac{1}{3}*\log_3x=0\\ \log_3x*(\frac{1}{2}*\log_3x-\frac{1}{3})=0\\ \begin{cases}\log_3x=0\\ \frac{1}{2}*\log_3x-\frac{1}{3}=0 \end{cases} \\ \begin{cases}x=1\\ \log_3x=\frac{2}{3} \end{cases} \\ \begin{cases}x=1\\ x=3^\frac{2}{3} \end{cases} \\](/tpl/images/0130/9512/1d8ad.png)
подставил в уравнение, ответы подошли, но среди списка нет
я не понял как прологарифмировал Marines и получил такой ответ (не разборчивое решение), но логарифмировать по основанию х не совсем корректно (с моей точки зрения). Область определения степенной функции х>0, а у логарифма основание >0 и не равно 1, т.е. искусственно сузил область определения, из рассмотрения выпал х=1, кстати, он подходит.
1 задание.
1)три целых пять двенадцатых(просто решаешь пример, все приводишь к общему знаменателю,и решаешь, сосчитать на калькуляторе)
2)три целых одиннадцать двадцать четвертых(все тоже самое)
2 задание.
1)x=-5,2(x=-2.8-2.4)
2)y=-1,76(y=18.24-20)
3)z=десять целых семнадцать двадцать седьмых(z=шесть целых пять девятых+ четыре целых две двадцать седьмых)(общий знаменатель 27 и считаешь.)
3 задание.
расстояние между точками ищеться их разностью.
расстояние между А и Б будет равно -5,2-(-1,8)=-5,2+1,8=-3,4(расстояние не может быть отрицательных, так что просто 3,4)
Расстояние между точками С и Д будет равно -две третьих-пять девятых(общий знаменатель 9)=-шесть девятых-пять девятых=-одиннадцать девятых(расстояние не может быть отрицательных, так что просто одиннадцать девятых=одна целая две девятых)
тут больше писать нечего, это самое расширеное решение
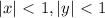
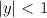 возвести в квадрат, получив,
возвести в квадрат, получив, 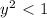 , что и требовалось проверить.
, что и требовалось проверить.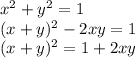
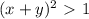
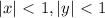 , следует, что 0 <x < 1, 0 < y < 1
, следует, что 0 <x < 1, 0 < y < 1
Прологарифмируем обе части уравнения по основанию х,получим log 3 (sqrt(x))=log x (3) + 1/2;
Упростим 1/2log 3 (x) = 1/(log 3 (x)) +1/2;
Введем подстановку t= log 3 (x);
Приводим квадратному уравнению: t^2/2=1+t/2;
t^2-t-2=0;Корни уравнения: -1;2
Log 3 (x) = 2;
x=9;
Log 3 (x) = -1;
x=1/3;
ответ: сумма равна 9(1/3)