7. Соберем дроби слева и приведем их к общему знаменателю.
Получим (4-4х-х+х²-х+5)/(х-5)(1-х)>0
После приведения подобных (х²-6х+9)/(х-5)(1-х)>0, последнее неравенство эквивалентно следующему
(х-3)²*(х-5)(1-х)>0
Решаем неравенство методом интервалов.
Приравняем к нулю левую часть найдем корни х=3; х=5; х=1, которые разбивают числовую ось на промежутки (-∞;1)∪(1;3)∪(3;5)∪(5;+∞)
Устанавливаем знаки на каждом из промежутков и выбираем те интервалы, где левая часть положительна.
ЭТо объединение промежутков (1;3)∪(3;5), Целые решения неравенства - числа 2; 4. их сумма равна 6
ответ 6
6. областью определения является все значения х, при которых квадратные корни имеет смысл, т.е. надо решить систему двух неравенств, а именно 15+3х>0,т.е. х>-5, и 2-9х≥0, откуда х≤2/9, Т.о. решением этой системы будет интервал (-5;2/9] Целых решений тут пять, а именно -4;-3;-2;-1;0
ответ 5
6) Подкоренное выражение корня чётной степени должно быть неотрицательным, то есть ≥ 0 , но если этот корень в знаменателе, то подкоренное выражение строго > 0 .
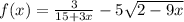
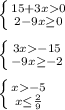
![x\in(-5;\frac{2}{9}]](/tpl/images/3209/6132/63cf1.png)
Всего 5 целых чисел : - 4 ; - 3 ; - 2 ; - 1 , 0
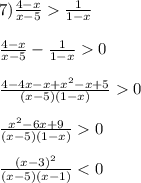
+ - - +
___________₀_________₀___________₀__________
1 3 5
////////////////// ///////////////////////
x ∈ (1 , 3) ∪ (3 ; 5)
Всего 2 целых решения : 2 ; 4
Их сумма равна : 2 + 4 = 6
чтобы узнать,какое уравнение имеет два корня -нужно их решить
a) -0,04+х^2=0.
x^2=0,04
x=0,2 <--- один корень
c) 6х^2+56=0.
6x^2=-56
x^2=-56:6
x^2=-9,(3) <--- против отношений, т.к.любое число возведенное в квадрат положительное
b)2x^2-5x+7=0.
D=(-5)^2-4*2*7=25-56=-31
D<0 - уравнение решений не имеет
x^-x+три четвертых=0
D=(-1)^2-4*1*3/4=1-3=-2
D<0 - уравнение решений не имеет
ответ:из данных утавнений никакое уравнение не имеет два корня
кажется так...