Объяснение:
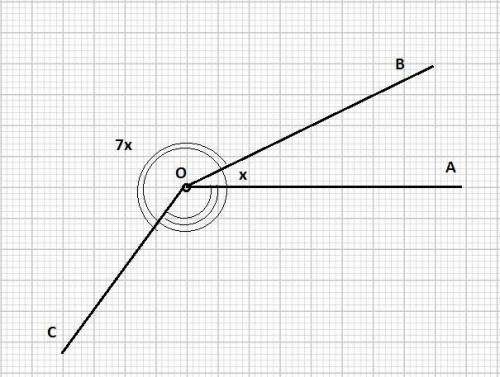
Сделаем чертеж.
Пусть наименьший угол равен x.
Тогда наибольший угол равен 7x.
1)
Пусть средний угол равен наименьшему.
Составим уравнение:
x+7x+x = 360°
9x = 360°
x = 40°
Поскольку углы выражены целыми числами, а наименьший должен быть меньше среднего, то x<40; x=39°
2)
Пусть средний угол равен наибольшему.
Составим уравнение:
x+7x+7x = 360°
15x = 360°
x = 24°
Поскольку углы выражены целыми числами, а наибольший должен быть больше среднего, то x>24; x=25°
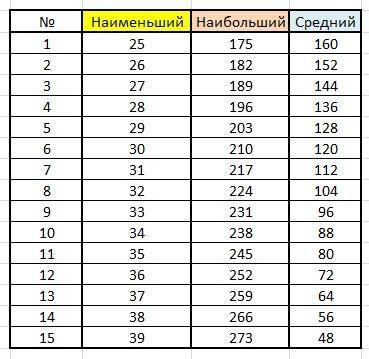
Итак, величина среднего угла лежит в интервале [25°; 39°].
Таких целых чисел 15. (смотри таблицу)
x+y=4 x^2 - y^2 = 8
y = 4 - x Подставляем x^2 - (4-x)^2 = 8
y = 4- x Подносим к степени. Присутствует форма сокращенного умножения. x^2 - (16 - 8х + x^2) = 8
y = 4 - x x^2 - 16 + 8x - x^2 = 8
y = 4-x x^2 Сокращается 8x = 8 + 16
y = 4 - x 8x = 24
y = 4 - x x = 3
Так как из второго уравнения системы мы уже знаем, чему равен ноль - также подставляем.
y = 4 - 3 x = 3
y = 1 x=3
(a1+2d)(a1+6d)=128
(12-4d+2d)(12-4d+6d)=128
(12-2d)(12+2d)=128
144-4d²=128
4d²=144-128
4d²=16
d²=4
1)d1=-2
a1=12+8=20
a5=a1+4d=12
S8=(2a1+7d)*8/2
S8=(40-14)*4=26*4=104
2)d=2
a1=12-8=4
S8=(8+14)*4=22*4=88