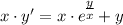
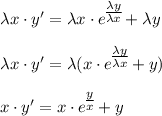
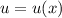с замены:
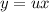, тогда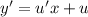 
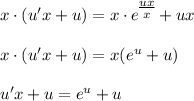
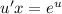
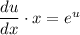- уравнение с разделяющимися переменными.
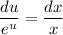- уравнение с разделёнными переменными.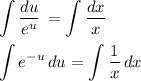
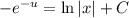- общий интеграл новой функции.
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: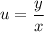 
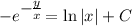- общий интеграл исходного уравнения.
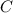. Подставим в общий интеграл начальное условие: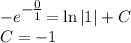
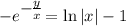- частный интеграл, также является решением данного дифференциального уравнения.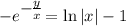
Сначала вынь корень из 25 будет 5. 5 умножить на 2=10. Теперь перемножаются корни из 2 и 8. Получается корень из 16 или просто 4 (вытащили корень). 10-4=6