D
Объяснение:
Фигура состоит из двух полукругов и одного квадрата .
Если сложить два полукруга - получим один круг.
Радиус полукругов = 6 ед.
Найдем площадь круга, составленного из двух полукругов:
S = πR²
S = π * 6² = π * 36 = 36π ед²
Теперь найдем площадь квадрата. Сторона квадрата = 12 ед
S = a²
S = 12² = 12 * 12 = 144 ед²
Сложим площади круга и квадрата :
36π + 144 ед²
Сейчас найдем площадь незакрашенного круга, который находится в центре. Диаметр этого круга равен стороне квадрата = 12 ед
D = 12 ед
S = πR²
R = D : 2
R = 12 : 2 = 6 ед
S = π * 6² = π * 36 = 36π ед²
И теперь найдем площадь заштрихованной фигуры. Вычтем из суммы площадей двух полукругов и квадрата, площадь незакрашенного круга который в центре :
36π + 144 - 36π = 144 ед²
Пример 1)
Разберёмся сначала с числителем:
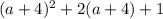
Для наглядности сделаем замену 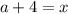 :
: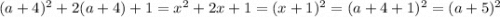
(мы использовали формулу квадрата суммы  в обратную сторону)
в обратную сторону)
Подставим:
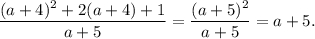
При этом мы должны записать ОДЗ 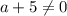 , чтобы не получилось деление на ноль.
, чтобы не получилось деление на ноль.
Пример 2)
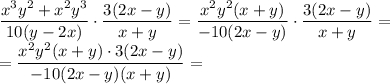
(перед тем, как сокращать, мы должны записать ОДЗ: 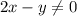 и
и 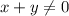 , чтобы не получилось деление на ноль):
, чтобы не получилось деление на ноль):
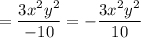
Пример 3)
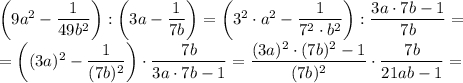
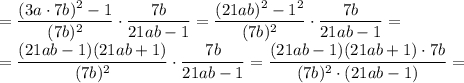
(перед тем, как сокращать, мы должны записать ОДЗ:  и
и  , то есть
, то есть  , чтобы не получилось деление на ноль):
, чтобы не получилось деление на ноль):

Пример 4)
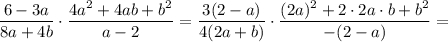
(в числителе второй дроби записано разложение квадрата суммы 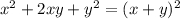 , поэтому получим следующее):
, поэтому получим следующее):
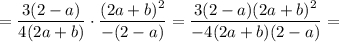
(перед тем как сокращать, мы должны записать ОДЗ: 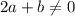 и
и 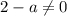 , чтобы не получилось деление на ноль):
, чтобы не получилось деление на ноль):
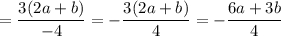
Если что-нибудь непонятно — спрашивай.
не за меня, а чтобы война закончилась.
наименьшая длинна промежутка - [15;16]