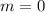Случайная величина Х - количество попаданий в кольцо. Случайная величина распределена по биномиальному закону. Вероятность успеха в одном испытании p = 0.1, тогда q = 1 - p = 0.9
1) Вероятность того, что баскетболист не попадает в кольцо ниразу
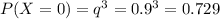
2) Вероятность того, что баскетболист попадет один раз
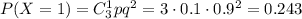
3) Вероятность того, что баскетболист попадет два раза
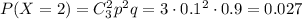
4) Вероятность того, что баскетболист попадет три раза
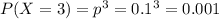
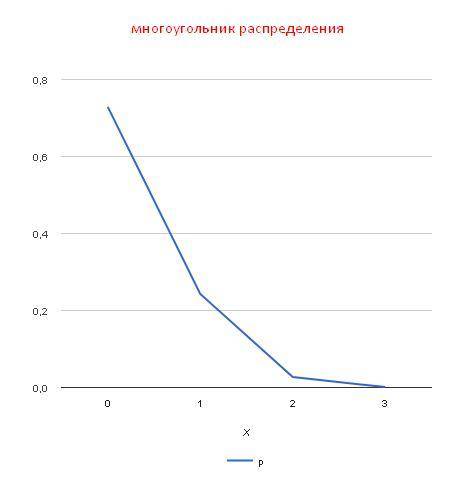
Закон распределения случайной величины X:
Xi 0 1 2 3
Pi 0.729 0.243 0.027 0.001
Математическое ожидание случайной величины X:
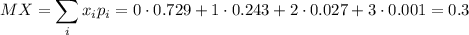
Иначе мат. ожидание можно подсчитать, если Х - распределена по биномиальному закону то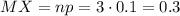 
Дисперсия случайной величины X:
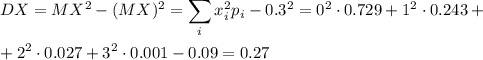
Иначе: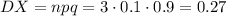 
Среднее квадратическое отклонение:
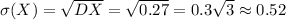
Графиком уравнения в любом случае будет прямая. Она не будет пересекать ось ординат только в том случае, если сама прямая будет параллельна ей.
В свою очередь прямая, параллельная оси ординат, имеет вид 
, где 
- какое-либо число. Заметим что здесь вообще не переменной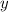 
.
Можно сделать вывод, что график не будет пересекать ось ординат тогда и только тогда, когда коэффициент перед 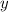- это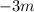 
- равен 0.
Т.е.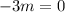 
, откуда 
.
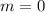Можем сделать проверку: подставляем 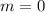в уравнение.
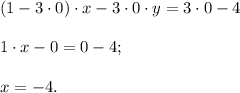
т.е. в итоге получили прямую, параллельную оси ординат.
ОТВЕТ:
