В решении.
Объяснение:
Постройте график функции
у= х³-2х²/(х-2)
по плану:
1) Во что превращается функция после упрощения?
у = (х²(х - 2))/(х - 2);
Сократить числитель и знаменатель на (х - 2), функция превращается в уравнение квадратичной функции у = х².
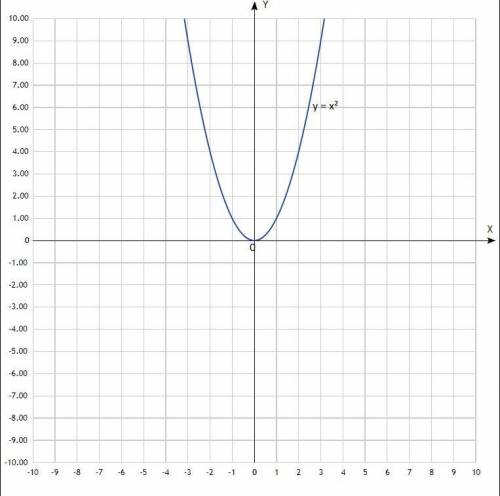
График - парабола с центром в начале координат (0; 0), ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 - 9
2) Написать область определения функции.
Область определения - это проекция графика функции на ось Ох.
Обозначается как D(f) или D(у).
Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.
Обычно запись: D(у) = R.
Но, так как х в знаменателе, по ОДЗ х не может быть равен 2, поэтому область определения данной функции - множество всех действительных чисел, кроме х = 2. В этой точке функция не определена.
D(у) = R : х ≠ 2.
3) ответ на вопрос: при каком значении а прямая у=а имеет с графиком ровно 2 общих точки ?
Согласно графика, при любом а > 0 (весь график выше оси Ох).
Объяснение:
|x -1| + |x +3| ≤ 4
Решим это неравенство методом интервалов.
Найдем нули подмодульных выражений:
х - 1 =0 → х = 1
х + 3 = 0 → х = - 3
Эти значения разбивают числовую ось на три интервала:
х ∈ (-∞; - 3] ; (-3; 1]; (1; + ∞)
Решим заданное неравенство на каждом из этих промежутков.
1) 1) x∈ (-∞; - 3], при этом неравенство примет вид:
- (х - 1) - (х + 3) ≤ 4
-х + 1 - х - 3 ≤ 4
-2х ≤ 6
х ≥ - 3
Пересекая найденное решение x∈ [- 3; +∞) c рассматриваемым интервалом x∈ (-∞; - 3] , получаем решение x = - 3
2) х ∈ (-3; 1]
- (х - 1) + х + 3 ≤ 4
0*х ≤ 4 → х - любое число. Учитывая интервал, х х ∈ (-3; 1]
3) х ∈ (1; + ∞)
х - 1 + х + 3 ≤ 4
2х ≤ 2
х ≤ 1 → х ∈ (- ∞; 1]
Для получения окончательного ответа объединим полученные решения:
x ∈ [- 3] ∪ (-3; 1] ∪ (- ∞; 1]
ответ: х ∈ [-3; 1]
Y наим=0
б) незнаю
в) Y наиб=18
Y наим=0
г)Y наиб=нету
Y наим=2