1) 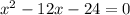

данное уравнение имеет два различных корня.
по теореме Виета:
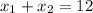

Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.
2) 

уравнение имеет два различных корня.
по теореме Виета:
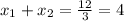
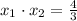
Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.
3) 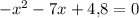
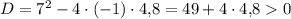
уравнение имеет два различных корня. По т. Виета:
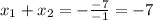
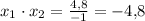
Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.
4) 

уравнение имеет два различных корня. По т. Виета:
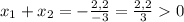
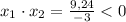
Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.
1) 11х = 36 - х
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование правой части уравнения:
36 - x = - ( x - 36)
Уравнение после преобразования:
11x = - (x - 36)
Упрощаем:
12x = 36
Сокращаем:
12(убираем)x = 12(убираем) * 3
x=3
2) 9х + 4 = 48 - 2х
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование правой части уравнения:
48 - 2x = -2 * (x - 24)
Уравнение после преобразования:
9x + 4 = -2 * (x - 24)
Упрощаем:
11x = 44
Сокращаем:
11(убираем)x = 11(убираем) * 4
x=4
3) 8 - 4х = 2х - 16
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование левой части уравнения:
8 - 4x = -4 * (x - 2)
Делаем преобразование правой части уравнения:
2x - 16 = 2 * (x - 8)
Уравнение после преобразования:
-4 * (x - 2) = 2 * (x - 8)
Упрощаем:
-6x = -24
Сокращаем:
-6(убираем)x = -6(убираем) * 4
x = 4
За остальным, если желаешь - в ЛС.
Пусть х км/ч - скорость первого автомобиля,
тогда х-9 км/ч - скорость второго автомобиля
Уравнение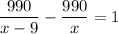
Скорости по условию не равны нулю, потому можно домножить обе части уравнения на произведение x(x - 9)
Скорость не может быть отрицательной, поэтому второй ответ не подходит.
ответ: скорость первого автомобиля 99 км/ч