а) вероятность того, что первый шар черный 5/7, вероятность, что второй шар черный 4/6, вероятность того, что вынуты два черных шара 5/7·4/6=10/21=0,476190..
б) вероятность того, что первый шар красный равна 2/7, вероятность ого, что второй шар красный равна 1/6, вероятность того, что оба шара красные равна
2/7·1/6=1/21=0,
в) вероятность того, что первый шар черный равна 5/7, вероятность того, что второй шар красный равна 2/6, вероятность того, что первый черный, второй красный равна
5/7·2/6=5/21
вероятность того, что первый шар красный равна 2/7, вероятность того, что второй шар черный равна 5/6, вероятность того, что первый шар красный, второй черный равна 2/7·5/6=5/21
вероятность того , что шары разных цветов равна 5/21+5/21=10/21=0,
ответ: 48.
Первый кол мы можем покрасить в любой из трех цветов (соблюдая условие задачи).
Второй кол мы можем покрасить только в 2 цвета (так как нам не следует соседние колья красить в один цвет).
Для третьего кола тоже остается 2 цвета (так как цвет 2-ого и 3-его кола не может совпадать).
С 4-ым и 5-ым колом похожая история: опять 2 цвета (для каждого из них).
А теперь, чтобы получить общее число нужно перемножить число для 1-ого, для 2-ого, ... , для 5-ого кольев:
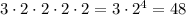
48 - это и есть ответ задачи!
3x-y=5
отнимем
5y=-12
y=-2,4
3x=5-2,4
3x=2,6
x=2,6:3
x=8 2/3
(8 2/3;-2,4)