ответ: 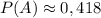 .
.
Объяснение:
В 1 урне 6 бел. и 4 чёрн. шаров, всего - 10 шаров.
Во 2 урне 4 бел. и 6 чёрн. шаров, всего - 10 шаров.
Найти вероятность события А={из 2 урны вынули белый шар } .
Гипотеза Н₁={из 1 урны вынули бел. шар} , P(H₁)=6/10 .
Переложив белый шар во 2 урну, в ней станет 11 шаров, из которых 5 белых и 6 чёрных.
Вероятность вынуть из 2 урны бел. шар равна Р(А/Н₁)=5/11 .
Гипотеза Н₂={из 1 урны вынули чёрн. шар} , Р(Н₂)=4/10 .
Переложив чёрный шар во 2 урну, в ней станет 11 шаров, из которых 4 белых и 7 чёрных.
Вероятность вынуть из 2 урны белый шар равна Р(А/Н₂)=4/11 .
По формуле полной вероятности вычисляем вероятность появления события А:
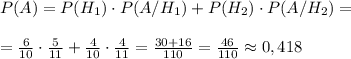
В каждой скобке разность квадратов
(60^2-59^2) + (58^2-57^2) +..+(2^1-1^2) = (60-59)(60+59) + (58-57)(58+57) +..+(2-1)(2+1) =
= 1(60+59) + 1(58+57) +..+1(2+1) = 60 + 59 + 58 + 57 +..+2 + 1
Получилась сумма чисел от 1 до 60, которая равна
60 + 59 + 58 + 57 +..+2 + 1 = (1 + 60)*60/2 = 61 * 30 = 1830