x км/ч скорость велосипедиста
х+25 км/ч скорость автомобилиста
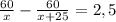
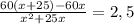
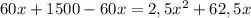
2,5x²+62,5x-1500=0 разделим на 2,5
х²+25х-600=0
D=625+2400=3025
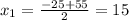 км/ч скорость велосипедиста
км/ч скорость велосипедиста
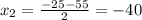 не удовлетворяет условию задачи
не удовлетворяет условию задачи
....................................................................................................................................................................................................................................................................................................................................................
Дано уравнение 3x⁴ + 10x³ +6x² + 10x +3 =0.
Попытаемся найти корень уравнения среди множителей свободного члена(1; -1; 3; -3). Подставив эти значения в уравнение, находим,что
х = -3 это корень уравнения.
Разделим заданное уравнение на (х + 3).
3x⁴ + 10x³ +6x² + 10x +3| x + 3
3x⁴ + 9x³ 3x³ + x² + 3x + 1
x³ + 6x²
x³ + 3x²
3x² + 10x
3x² + 9x
x + 3
x + 3
0.
Полученный результат 3x³ + x² + 3x + 1 перекомпануем:
(3x³ + 3x) + (x² + 1) = 3x(x² + 1) + (x² + 1) = (3x + 1)(x² + 1).
Таким образом, левую часть исходного уравнения можно представить в виде произведения : (x + 3)(3x + 1)(x² + 1) = 0.
Отсюда видим, что это уравнение имеет 2 очевидных корня:
х = -3 и х = -1/3. Последний множитель не может быть равен нулю.
Тогда ответ: произведение корней равно -3*(-1/3) = 1.
cos(8x-π/8)≥√3/2
2πn-π/6≤8х-π/8≤2πn+π/6, n∈Z
2πn-π/6+π/8≤8х≤2πn+π/6+π/8
2πn-π/24≤8х≤2πn+7π/24
πn/4-π/192≤х≤πn/4+7π/192
x∈[πn/4-π/192; πn/4+7π/192]