пояснения прилагаю.
1) 1.
⅓ =
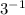
отсюда: - 1 × (x + 1) = - x - 1
2. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
2) 1. выносим общий множитель за скобку, используя одно из свойств показательных выражений:
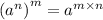
2. делим выражение на коэффициент при x
3. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
3) 1. преобразовав выражение (от перемены мест множителей проивзедение не меняется),
можно сделать замену, приводящую уравнение к квадратному.
первый корень: x ∉ R, так как значения показательной функции всегда положительны (иными словами, если строить график, то ни x, ни y никогда не будут принимать отрицательные значения).

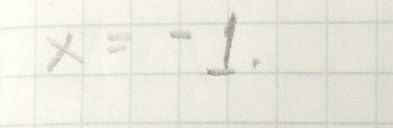
a₁₇=a₁+16*d=2
S₂₁=(2a₁+20*a₁*d)*21/2=(42*a₁+420*d)/2=21*a₁+210*d
S₁₂=(2a₁+11*a₁*d)*12/2=(24*a₁+132*d)/2=12*a₁+66*d
S₂₁-S₁₂=21*a₁+210*d-12*a₁-66*d=9*a₁-144*d=9*(a₁-16*d) ⇒
S21-S12=9*2=18.
ответ: S₂₁-S₁₂=18.