Так как нужно найти нули, то есть корни, мы приравняем x^3+4x^2+x-6 к 0
нужно найти все целые делители свободного члена, то есть числа -6
+-1,+-2,+-3,+-6;
заметим, что при постановке вместо х числа 1, равенство получается верным (0=0)
значит число 1 является одним из корней уравнения!
Но как же найти остальные 2?
Если число 1является корнем, то его можно записать так : (х-1)
для того чтобы найти оставшиеся два корня нужно разделить (x^3+4x^2+x-6) на (х-1)
думаю деления подобного родна проходили в школе:)
при делении получается : х^2+5х+6; по теореме виета найдем сразу корни : х=-3;-2
ответ: -3;-2;1
Покажем, что (cos x)'=-sin x
По определению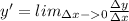 
Приращение функции равно
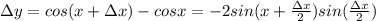
Ищем отношение
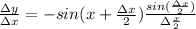
Перейдем в этом равенстве к границе, когда 
. В следствии непрерывности функции sin x
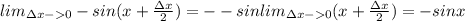
Для второго множителя (используя один из замечательных пределов), обозначив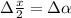 
, имеем
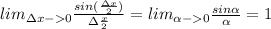
Поєтому
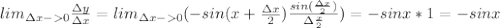
Т.е. (сos x)'=-sinx
Производная тангенса. Возьмем любую точку х є (a;b), где (a;b) - один из интервалов, на котором определена функция tg x. Ищем приращение
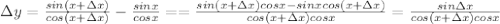
Получаем отношение
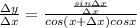
переходим к границе, когда .
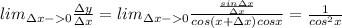
Следовательно производная функции y=tg x существует и равна
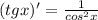
18^2-12·6= 324-72=252.
12ху ввели дополнительно, чтобы получился квадрат, 12ху прибавили и отняли чтобы не изменилось начальное выражение.