а). В этом числе ноль встречается 9 раз, а числа 2, 3, 9 - по 20 раз.
б). Да, 123...9899 делится на 9.
Сначала посчитаем, сколько всего в числе 1234..9899 было выписано цифр 0, 1, 2, 3, 9. Это тоже самое, что и посчитать, сколько раз встречаются эти же цифры в числах от 1 до 99.
Цифра 0:
10, 20, 30, 40, 50, 60, 70, 80, 90 - всего 9 раз.
Цифра 1:
1, 10 - 19 (11 раз), 21, 31, 41, 51, 61, 71, 81 ,91 - всего 20 раз.
Понятно, что 2, 3, 9 встречаются столько же раз, сколько и 1 (все они могут стоять 10 раз в разряде единиц, и 10 раз - в разряде десятков).
Теперь нужно узнать, делится ли число 1234..9899 на 9.
Признак делимости на 9: число делится на 9 тогда и только тогда, когда сумма его цифр тоже делится на 9.Так что мы должны узнать, делится ли 1 + 2 + 3 + ... + 99 на 9.
Для этого найдем искомую сумму по формуле арифметической прогрессии:
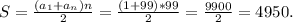
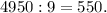
Так как получилось разделить нацело, то 1234...9899 делится на 9.
Здесь воспользуемся тем, что значение выражения не изменится, если его одновременно домножить и разделить на одно и то же число. Домножим и разделим выпражение на cos 10:
(16sin10 * cos 10 * cos 20 * cos 40 * cos 60) / cos 10 = (8 * 2sin10 * cos 10 * cos 20 * cos 40 * cos 60) / cos 10 = (8sin 20 * cos 20 * cos 40 * cos 60) / cos 10 = (4 * 2sin20 * cos 20 * cos 40 * cos 60) / cos 10 = (4sin 40 * cos 40 * cos 60) / cos 10 = (2sin80 * cos 60) / cos 10 = (2sin 80 * 0.5) / cos 10 = sin 80 / cos 10.
Далее воспользуемся формулами приведения.
sin(90 - 10) / cos 10 = cos 10 / cos 10=1
2) m²-a²=(m-a)(m+a)
3) a²-3²y²=(a-3y)(a+3y)
4) 7²x²-11²a²=(7x-11)(7x+11)
5) x²y²-1=(xy-1)(xy+1)