1. 3)
2. а) x=-24
б) x=30
3. 19 книг на 1 полке
34 книги на второй полке
4. а=-1/3
5. s=800 кв.м- площадь
Объяснение:
1) -2x+1=-x-6
-2x+x=-6-1
-x=-7
x=7
2) a) -1x=24 б) 1,2х+3,7=0,7-3,7
-x=24 1,2х-1,3х=0,7-3,7
x=-24 -0,1х=-3
х=30
3. пусть на первой полке а книг, тогда на второй а+15 книг
а+а+15=53
2а=38
а=19
19 книг на 1 полке
34 книги на второй полке
4. 4а+8 на 3 больше 3-2а
(4а+8)-(3-2а)=3
6а=-2
а=-1/3
ответ: а=-1/3
5. Р прямоугольника=2*(а+в)
х- ширина, 2х-длина
2*(х+2х)=120
3х=120/2
3х=60
х=60/3
х=20
20м- ширина, 2*20=40м-длина
S=a*b=20*40=800 кв.м- площадь
1)
-2x+1=-x-6
-2x+x=-6-1
-x=-7 | -1
x=7
2)a
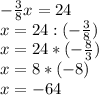
2)b
2(0.6x+1.85) = 1.3x+0.7
1.2x+3.7=1.3x+0.7
1.2x-1.3x=0.7-3.7
-0.1x=-3 |-1
0.1x=3
x=3:0.1
x=30
3)
Первая полка - (x+15) книг
Вторая полка - (x) книг
Всего - 53 книг
x+15+x=53
2x=53-15
2x=38
x=38:2
x=19
=>Первая полка -> 19+15=34
=>Вторая полка -> 19
=>Всего -> 34+19=53
4)
(4a+8)-(3-2a)=3
4a+8-3+2a=3
6a=-2
a=-1/3
5)
Ширина - x
Длина - 2x
Р = 2х + 2х + х + х
120 = 2х + 2х + х + х
120 = 6х
х = 120/6
х = 20
Ширина = 20см
Длина = 20*2=40
S - площадь
S = 20*40
S = 800 см^2
2sin(2x) - 2 + √2 + 1 = (√2 - 1)(sin x - cos x)
Придумал, как решить!
2sin(2x) - 2 = -2(1 - sin(2x)) = -2(sin^2 x - 2sin x*cos x + cos^2 x) =
= -2(sin x - cos x)^2
Подставляем
-2(sin x - cos x)^2 + √2 + 1 = (√2 - 1)(sin x - cos x)
2(sin x - cos x)^2 + (√2 - 1)(sin x - cos x) - (√2 + 1) = 0
Замена sin x - cos x = y
2y^2 + (√2 - 1)y - (√2 + 1) = 0
Решаем квадратное уравнение
D = (√2 - 1)^2 - 4*2(-(√2 + 1)) = 2 - 2√2 + 1 + 8(√2+1) = 11 + 6√2 =
= 2 + 9 + 2*3√2 = (3 + √2)^2
x1 = (1 - √2 - 3 - √2)/4 = (-2 - 2√2)/4 = -(1 + √2)/2 ~ -1,2 > -√2
x2 = (1 - √2 + 3 + √2)/4 = 4/4 = 1
Обратная замена
y = sin x - cos x = √2*(1/√2*sin x - 1/√2*cos x) =
= √2*(sin x*cos(pi/4) - cos x*sin(pi/4)) = √2*sin(x - pi/4)
Поскольку sin a ∈ [-1; 1], то √2*sin(x - pi/4) ∈ [-√2; √2]
Оба корня попадают в этот промежуток.
1) √2*sin(x - pi/4) = -(1 + √2)/2
sin(x - pi/4) = -(1 + √2)/(2√2) = -(√2 + 2)/4
x1 = pi/4 - arcsin((√2 + 2)/4) + 2pi*k
x2 = 3pi/4 + arcsin((√2 + 2)/4)) + 2pi*k
2) √2*sin(x - pi/4) = 1
sin(x - pi/4) = 1/√2
x3 = pi/4 + pi/4 + 2pi*n = pi/2 + 2pi*n
x4 = pi/4 + 3pi/4 + 2pi*n = pi + 2pi*n