1) После раскрытия скобок выражение принимает вид:
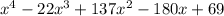 .
.
Эта функция имеет 2 минимума:
1. (0,8; 1,8)
2. (10,2; -36).
2) Запишем пропорцию - a/b = c/d a = b + 6 c = d + 5
(b + 6) / b = (d + 5) / d Отсюда 6d = 5b d = 5b / 6
По условию a^2 + b^2 + c^2 + d^2 = 793
Подставив значения, получим - (b + 6)^2 + b^2 + (d + 5)^2 + d^2 = 793.
После раскрытия скобок - 2b^2 + 12b + 2d^2 + 10d + 61 = 793/
Заменив d = 5b / 6 и приведя к общему знаменателю, получим
72b^2 + 432b + 50b^2 + 300b = 26352 или 122b^2 + 732b - 26352 = 0
Корни этого уравнения равны -18 и 12. Отрицательное значение отбрасываем - b = 12.
а =12 + 6 = 18 - это первый член пропорции
(100000+x) - первоначальное число
(10х+1) - число, которое получено из первого путём перемещения первой слева единицы на последнее место.
По условию полученное число в 3 раза больше первоначального,
Уравнение
10х+1 = (100000+х) *3
10х+1 = 300000 + 3х
10х-3х = 300000 - 1
7х=299999
х=299999 : 7
х=42857
142857 - первоначальное число
428571 - число, которое получено из первого путём перемещения первой слева единицы на последнее место.
Проверка
428571 : 3 = 142857
142857 = 142857 - верное равенство.
ответ: 142857 - первоначальное число.
На отрезке (-1;1) это будет минимальное значение функции при х = 0.
Влево и вправо от точки х = 0 значения функции возрастают.
х = -1, х = 1 у = (-1)² + 5 = 6,
у = 1² + 5 = 6.
ответ: на отрезке х=(-1; 0) у=(6; 5),
на отрезке (0; 1) у=(5; 6).