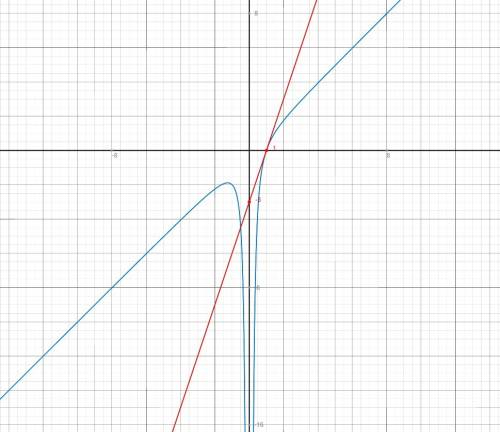
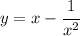параллельно прямой 
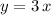будет выглядеть следующим образом: 
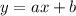, где a - коэффициент наклона касательной, он равен по условию 3, так как прямая параллельна прямой 
.
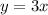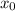равна углу наклона касательной данной функции в этой точке, то, приравняв производную к данному коэффициенту наклона (k = 3), найдем точку касания.
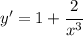. Приравняем её к 3 и получим: 
. 
.
.
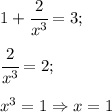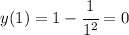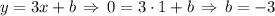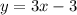
1) -31; -28; -25…
an = a₁ + d*(n - 1)
a₁ = - 31
a₂ = - 28
d = a₂ - a₁
d = - 28 - (- 31) = 3
a₃₀ = - 31 + 3*(30 - 1) = - 31 + 3*29 = 56
2) -1; 3; -9…
b₁ = - 1
b₂ = 3
q = b₂ / b₁
q = 3/(-1) = - 3
b₇ = b₁ * q⁶
b₇ = - 1 * (-3)⁶ = - 729