"за три дня выручка продовольственного магазина составила 18 000 рублей. известно, что выручка в понедельник на 3 000 рублей меньше, чем во вторник, и в два раза больше выручки, полученной магазином в среду. найдите, какая выручка
была в магазине в понедельник." пусть х рублей-выручка, полученная магазином в среду. составьте уравнение, соответствующее условию
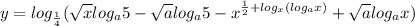
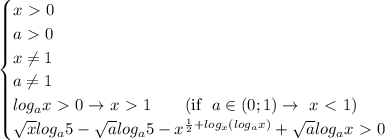
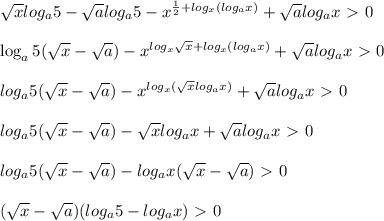
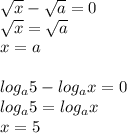
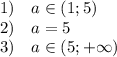
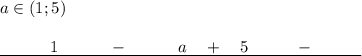
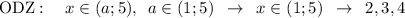
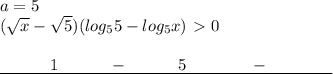

![\text{ODZ:}\quad x\in(5;a)\quad \rightarrow \quad 6,7,8,9\quad \rightarrow a\in(9;10]](/tpl/images/0832/0487/bd5ab.png)
![\boxed{a\in(9;10]}](/tpl/images/0832/0487/fff13.png)
х - в среду
2х - в понедельник
2х+3000 - во вторник
х+2х+2х+3000=18000
5х=15000
х=15000/5
х=3000 - в среду
2*3000=6000 - в понеделник
2*3000+3000=9000 - во вторник