Найти наибольшее и наименьшее значение функции на промежутке: 1) f(x)=x^2-2x-3 [-5; 1/2]; 2) f(x)=x^2-5x+6 [0; 3]

👇

Ответ:

crasavchik

07.11.2021

1) f(x)=x² -2x-3
f ' (x)=2x-2
2x-2=0
2x=2
x=1
x=1 не входит в промежуток [-5; 1/2].

f(-5)=(-5)² -2*(-5) -3=25 +10-3=32 - наибольшее
f(1/2)= (1/2)² -2*(1/2) -3= (1/4) - 1 -3= (1/4) -4 = -3 ³/₄ - наименьшее

2)
f(x)=x²-5x+6
f ' (x)=2x-5
2x-5=0
2x=5
x=2.5∈[0; 3]

f(0)=0² - 5*0 +6 =6 - наибольшее
f(2.5)= 2.5² - 5*2.5 +6=6.25 - 12.5 +6= -0.25 - наименьшее
f(3) =3² -5*3 +6=9-15+6=0

4,5(34 оценок)

Открыть все ответы

Ответ:

hjhytu

07.11.2021

По определению, 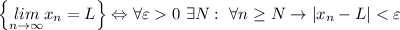$\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 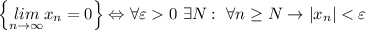$\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

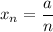
2) $x_n=\dfrac{a}{n}$

|x_n|

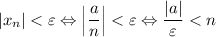
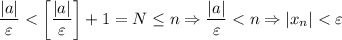
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

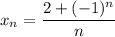
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

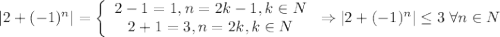
$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда 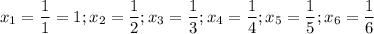$x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$

___________________________

Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 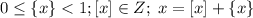$0\leq \{x\}$

пример 2 и 4. Все теоремы и аксиомы, будьте добры, распишите. Действий, пусть и банальных, легких не

4,6(34 оценок)

Ответ:

Lizok2509

07.11.2021

«Молитва это вульгаризованная и рационалистически разжиженная позднейшая форма чего-то очень энергичного, активного и сильного: магического заклинания, принуждения бога» (Т. Манн)

Самая первая, самая красивая, мелодичная часть этой повести – молитва героя. Именно такая молитва, не тихая христианская но убеждение, заклинание, попытка слабого, потерянного человека принудить судьбу измениться. Во имя его любви.

При том, такой любви, в которую очень поверить первой любви, в которой разом встретилась та самая девушка, румяная, взволнованная, очень юная «Она» – и еще весна, цветущие деревья, красота мира, воспринятая молодой, впечатлительной душой, и еще вера в светлое будущее, наивная за него борьба. Все то, что было у него и все, что отняли разом. Сама жизнь, которую он потерял, которую нельзя уже вернуть, но он верит, что можно, с одной единственной нити, с Нее, в образ которой измученно сердце соединило все светлое, что сумело сохранить.

Но Бог, в которого герой никогда прежде не верил, конечно, не внемлет молитве и карает героя за нее, не то чтобы жестоко стирает с лица земли, прекращая разом и надежды и муки. Вообще, у Грина очень интересен мотив «молитвы», она предстает, как заклинание, которое может читать лишь избранный. Для всех же остальных это слабость, непозволительное покушение на божественные сферы. Так и здесь. Молитва сломанного тюрьмой человека, искренняя, жалобная, тихая, у которой недостаточно силы, чтобы заставить Бога покориться человеческой воле.

«У него была одна молитва, только одна…»

4,4(30 оценок)

Это интересно:

Компьютеры-и-электроника

08.07.2020

Как скачать фильм с YouTube через YouTube Downloader...

Компьютеры-и-электроника

25.12.2021

Как правильно отправлять SQL запросы в Mysql из командной строки...

Хобби-и-рукоделие

29.03.2020

Mountain Dew: Как сделать свечение...