Объяснение:
1.
1) (6x-7)/(x-2) -(x+8)/(x-2)=0
(6x-7-x-8)/(x-2)=0
(5x-15)/(x-2)=0
x-2≠0; x₁≠2
5x-15=0 |5
x-3=0; x₂=3
ответ: 3.
2) x/(x+6) -36/(x²+6x)=0
x/(x+6) -36/(x(x+6))=0
(x²-36)/(x(x+6))=0
x₁≠0
x+6≠0; x₂≠-6
x²-36=0
(x-6)(x+6)=0
x-6=0; x₃=6
x+6=0; x₄=-6 - этот корень не подходит для уравнения, так как x₂≠-6 (что означает - знаменатель не может быть равен нулю).
ответ: 6.
2.
1) 275000=275·10³=2,75·10⁵
2) 0,0028=0,28·10⁻²=2,8·10⁻³
3.
1) b⁻⁶·b⁴=b⁻⁶⁺⁴=b⁻²=1/b²
2) b²÷b⁻⁷=b²⁻⁽⁻⁷⁾=b²⁺⁷=b⁹
3) (b⁻⁵)⁻²·b⁻⁸=b¹⁰·b⁻⁸=b¹⁰⁺⁽⁻⁸⁾=b¹⁰⁻⁸=b²
4.
0,4a¹⁴b⁻⁹·1,6a⁻⁸b¹⁷=2/5 ·8/5 ·a¹⁴⁻⁸b⁻⁹⁺¹⁷=16/25 ·a⁶b⁸=(16a⁶b⁸)/25
1) на множестве R и С:
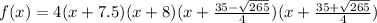
На множестве Q:
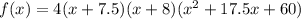 .
.
2) на множестве Q, R и С:
g(x)=(x-3)²(x+5)
Объяснение:
чтобы разложить многочлен axⁿ+bxⁿ⁻¹+cxⁿ⁻2+... на множители, нужно найти его нули и записать разложение в виде: a(x-x₁)(x-x₂)(x-x₃)..., где x₁, x₂, x₃, .... - корни (нули) многочлена.
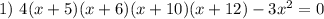
перемножим почленно 1 скобку с 4-й, а 2-ю с 3-й:
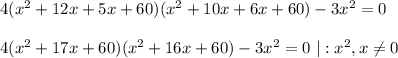
Разделим всё уравнение на x²
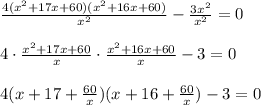
Делаем замену:
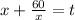
Тогда
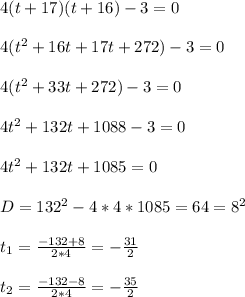
Обратная замена:
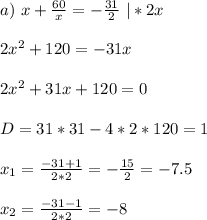
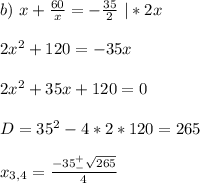
Разложение на множестве R и C будет следующим:
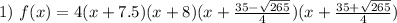
2) корни x₃ и x₄ не являются рациональными (нельзя представить в виде обыкновенной дроби), тогда
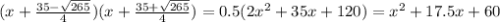
И разложение на множестве Q будет выглядеть:
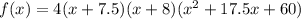 .
.
2) Теперь разбираемся со вторым многочленом:
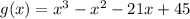
Находим рациональный корень по схеме Горнера.
Путем перебора делителей свободного члена (числа 45) получаем x₁=-5 (см. рисунок)
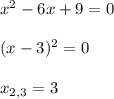
Таким образом разложение на Q, R и C будет:
g(x)=(x-3)²(x+5)
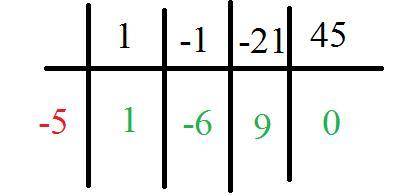
-b=x1+x2
5=-3+x2
x2=5+3=8
q=x1*x2
q=-3*8=-24