выпишем координаты данных векторов:
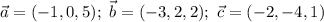
a)
координаты:
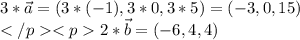
скалярное произведение векторов - число:
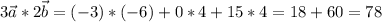
б)
координаты:
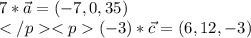
векторное произведение векторов - вектор, находим его координаты:

находим модуль(длину) полученного вектора:
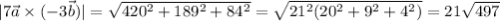
в)
координаты:
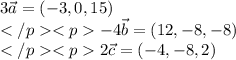
смешанное произведение векторов - число, находим его:
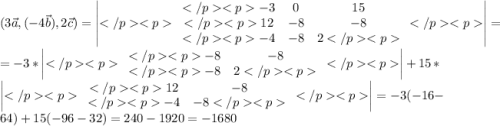
г)
Координаты:
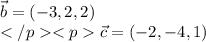
Векторы коллинеарны, если их соответствующие кординаты пропорциональны
Проверим это утверждение:
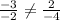
Данное равенство неверно, значит векторы b и c не коллинеарны
Векторы ортогональны, если их скалярное произведение равно нулю.
Проверим это утверждение:
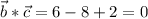
- верно, значит данные векторы ортогональны
Векторы b и c ортогональны
д)
Координаты:
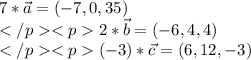
Три вектора компланарны, если их смешанное произведение равно нулю.
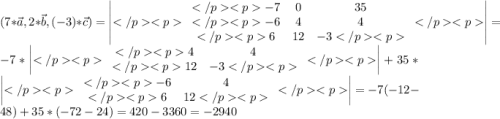
-2940 не равно нулю => данные векторы не компланарны.
выпишем координаты данных векторов:
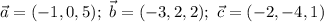
a)
координаты:
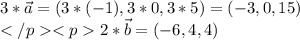
скалярное произведение векторов - число:
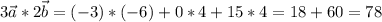
б)
координаты:
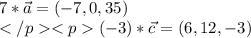
векторное произведение векторов - вектор, находим его координаты:

находим модуль(длину) полученного вектора:
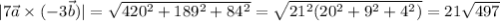
в)
координаты:
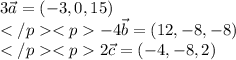
смешанное произведение векторов - число, находим его:
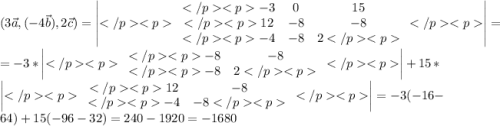
г)
Координаты:
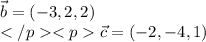
Векторы коллинеарны, если их соответствующие кординаты пропорциональны
Проверим это утверждение:
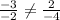
Данное равенство неверно, значит векторы b и c не коллинеарны
Векторы ортогональны, если их скалярное произведение равно нулю.
Проверим это утверждение:
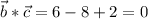
- верно, значит данные векторы ортогональны
Векторы b и c ортогональны
д)
Координаты:
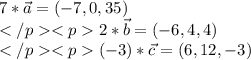
Три вектора компланарны, если их смешанное произведение равно нулю.
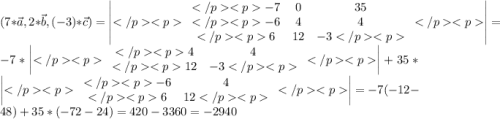
-2940 не равно нулю => данные векторы не компланарны.
Найдем дискриминант квадратного уравнения:
D=b2-4ac=(-7)^2-4*1*10=49-40=9
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1=(7-√9)/2*1=(7-3)/2=4/2=2x2=(7+√9)/2*1=(7+3)/2=10/2=5