1. Найти наибольшее и наименьшее значение функции
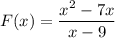на промежутке [-4; 1]
Точка разрыва x=9 в заданный интервал не входит.
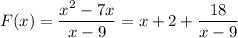
Первая производная для нахождения точек экстремумов.
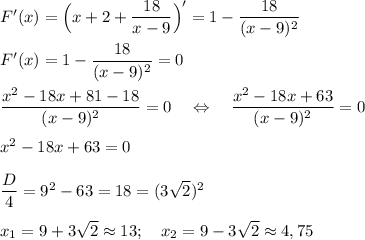
Обе точки экстремумов не попадают в интервал x∈[-4; 1]
Значения функции на концах интервала
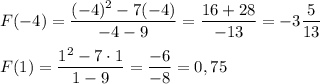
ответ: наименьшее значение функции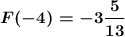 
;
наибольшее значение функции F(1) = 0,75
-----------------------------------------------------------------------------
2. Записать уравнение касательной к графику
функции F(x)=x⁴-2x в точке x₀=-1
Уравнение касательной имеет вид y = F(x₀) + F’(x₀)·(x - x₀)
F(-1) = x⁴-2x = (-1)⁴ - 2(-1) = 1+2 = 3
F'(-1) = (x⁴-2x)' = 4x³ - 2 = 4(-1)³ - 2 = -6
y = F(x₀) + F’(x₀)·(x - x₀) = 3 - 6 (x + 1) = 3 - 6x -6 = -6x - 3
ответ: уравнение касательной y = -6x - 3
---------------------------------------------------------------------------
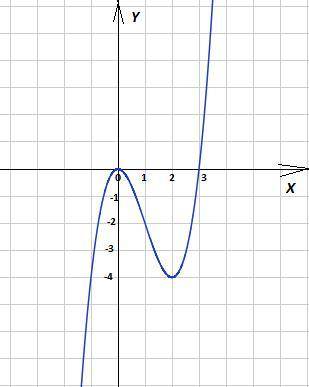
3. Исследовать функцию и построить ее график F(x)=x³-3x²
1) Область определения D(F) = R
2) Область значений E(F) = R
3) Нули функции
F(x)=x³-3x² = 0; x²(x - 3) = 0; x₁ = 0; x₂ = 3
4) Пересечение с осью OY
x = 0; F(0) = 0³-3·0² = 0
5) Экстремумы функции
F'(x) = 0; (x³-3x²)' = 0; 3x² - 6x = 0; 3x(x - 2) = 0;
x₁ = 0; F(0) = 0; F"(0) = 6x - 6 = -6 ⇒ локальный максимум.
x₂ = 2; F(2) = 2³-3·2² = -4; F"(2) = 6x - 6 = 6 ⇒ локальный минимум.
6) Монотонность функции.
Интервалы знакопостоянства первой
производной F'(x) = 3x(x - 2)
++++++++ (0) ------------- (2) +++++++++> x
/ \ /
x ∈ (-∞; 0)∪(2; +∞) - функция возрастает
x ∈ (0;2) - функция убывает
7) Функция не периодическая, общего вида (не является чётной, не является нечётной).
8) Дополнительные точки для построения
x₃ = -1; y₃ = -4; x₄ = 1; y₄ = -2
9) График функции в приложении
In the evenings into the city and go clubbing or see a movie. a lot of new friends. my pronunciation is much better already, and almost everything. On weekdays Liam. At the moment on their new website and help with it. some useful stuff about how people business in this country.
to see me? the winter holiday skiing with Ryan and Liam. to meet you and there’s plenty of space. You must bring lots of warm clothes because really cold here in the winter. Let me know as soon as . And tell me what these days.
Сумма первых трёх членов геометрической прогрессии вычисляется по формуле:
S(3) = b1(q³ - 1) / (q-1)
По осномвному свойству пропорции:
S(3) * (q-1) = b1(q³-1)
6.2(q³-1) = 80.6 * (q-1)
Разделим обе части уравнения на 6.2:
q³-1 = 13(q-1)
(q³ - 1) - 13(q-1) = 0
(q-1)(q² + q + 1) - 13(q-1) = 0
(q-1)(q² + q + 1 - 13) = 0
q - 1 = 0 или q² + q + 1 - 13 = 0
q = 1 q² + q - 12 = 0
q1 = -4; q2 = 3
Решая кубическое уравнение, мы получили, что знаменатель может быть равен одновременно и 1, и -4, и 3. Такого, естественно, быть не может. Поэтому определим тот знаменатель, который нам нужен, просто подставив его в формулу для расчёта суммы 3 первых членов.
6.2(1³ - 1) / (1 - 1) явно не равно 80.6(более того, это выражение даже не имеет смысла, поскольку знаменатель при q = 1 обращается в 0). Значит, значение q = 1 нам не подходит. Продолжим проверку.
Пусть q = 3, тогда подставляя, получаем следующее:
6.2(3³ - 1) / (3 - 1) = 6.2 * 26 / 2 = 80.6 - как раз то, что нам нужно. Но проверим на всякий случай q = -4.
6.2((-4)³ - 1) / (-4 - 1) = 6.2 * (-65) / (-5) = -403 / (-5) = 80.6 - сюрпризец
Подсчёты показали, что возможны аж два варианта знаменателя, чего никак нельзя было ожидать. Таким образом, q = 3 или q = -4
Теперь найдём b3. Вполне очевидно, что будут тоже 2 значения.
b3 = b1q² = 6.2 * 3² = 6.2 * 9 = 55.8 - это первый вариант
b3 = 6.2 * (-4)² = 6.2 * 16 = 99.2 - вторая возможность
Таким образом, возможны два варианта прогрессии.