Рассмотрим последние цифры степеней чисел 3 и 7 (очевидно, степени чисел 33 и 77 оканчиваются на те же цифры; в таблице последняя цифра числа x обозначена как x mod 10):
Дальше таблицу можно не продолжать: поскольку последняя цифра степени определяется только последней цифрой предыдущей степени, то дальше всё будет повторяться: например, для степеней тройки дальше идут 3, 9, 7, 1, 3, 9, ... Таким образом, последовательность последних цифр степеней тройки и семёрки является периодической с периодом 4, то есть прибавление любого количества четвёрок к показателю степени последнюю цифру не меняет.
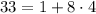, поэтому 
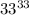оканчивается на ту же цифру, что и 
, то есть на 3. 
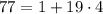, поэтому 
оканчивается на ту же цифру, что и 
, то есть на 7. Значит, сумма 
оканчивается на ту же цифру, что и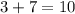 
, то есть на 0. Искомый остаток равен нулю.
ответ. 0
1/x(x+2)+2/(x+1)²=2 ; * * *ОДЗ x ∉{ -2 ;-1;0 } * * *
1/(x²+2x) +2/(x²+2x+1) =2; * * * замена t =x²+2x * * *
1/t +1/(t+1) =2 ;
t+1 +t =2t(t+1) ⇔2t²=1 ⇒t =±1/√2.
а)x²+2x = -1/√2⇔x²+2x +1/√2 =0 (не имеет действительных корней).
б)x²+2x =1/√2 ⇔x²+2x -1/√2 =0 ⇒x= -1± √(1+1/√2).
2)
1,5+1≤ lx-1l * * * ??? * * *
lx-1l ≥2,5 ⇔[ x-1≤ -2,5 ; x-1≥2,5 .⇔[ x≤ -1,5 ; x ≥ 3,5.
ответ: x∈ (-∞; -1,5] ∪ [3,5;∞).
3)
log_5 (2x-3)/ log_1/3 log_3 9 >0 ;
log_5 (2x-3)/ log_1/3 2 >0 ; * * *т.к. 0<1/3<1 ,то log_1/3 2 < 0 * * *
log_5 (2x-3) < 0 * * * т.к. 5>1 ,то
⇔0< 2x-3 <1⇔ 3<2x< 4 ⇔3/2 <x<2.
ответ: x∈ (1,5;2).