Алгебра: Решите систему неравенств {х-3у=2 и {ху+у=6

Решите систему неравенств {х-3у=2 и {ху+у=6

👇

Увидеть ответ

Ответ:

Maowsk

31.07.2021

х-3у=2

ху+у=6

С первого выразим х:

х=2+3у

Подставим во второе уравнение

(2+3у) у+у=6

2у +3у^2 +y = 6

3y^2+3y-6=0

y^2+y-6=0

y1= 1

y2= - 2

Теперь найдём х1 и х2:

y1= 1, тогда х1=2+3*1=5

y2= - 2 , тогда х2=2+3*(-2)= 2-6=-4

ответ: (5;1) и (-4; -2)

4,8(56 оценок)

Открыть все ответы

Ответ:

Qwerty23459484

31.07.2021

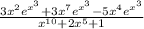
$\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{x^{10}+2x^{5}+1}$

Объяснение:

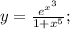
$y=\frac{e^{x^{3}}}{1+x^{5}};$

Производная дроби находится по следующей формуле:

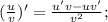
$(\frac{u}{v})'=\frac{u'v-uv'}{v^{2}};$

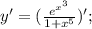
$y'=(\frac{e^{x^{3}}}{1+x^{5}})';$

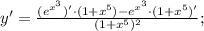
$y'=\frac{(e^{x^{3}})' \cdot (1+x^{5})-e^{x^{3}} \cdot (1+x^{5})'}{(1+x^{5})^{2}};$

Функция

$e^{x^{3}}$

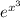
является сложной функцией. Производная сложной функции находится по следующей формуле:

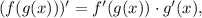
$(f(g(x)))'=f'(g(x)) \cdot g'(x),$

отсюда получаем

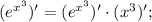
$(e^{x^{3}})'=(e^{x^{3}})' \cdot (x^{3})';$

Если ввести замену

$t=x^{3},$

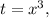
то выражение

$e^{x^{3}}$

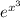
преобразуется как

$e^{t}.$

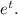
Производная последнего выражения является табличным значением:

$(e^{t})'=e^{t};$

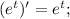
Возвращаясь к замене, получаем:

$e^{x^{3}}.$

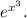
Производная второго множителя находится по следующей формуле:

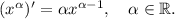
$(x^{\alpha})'=\alpha x^{\alpha-1}, \quad \alpha \in \mathbb {R}.$

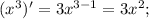
$(x^{3})'=3x^{3-1}=3x^{2};$

Подставим полученные значения в произведение:

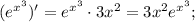
$(e^{x^{3}})'=e^{x^{3}} \cdot 3x^{2}=3x^{2}e^{x^{3}};$

Подставим значение этой производной в дробь:

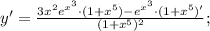
$y'=\frac{3x^{2}e^{x^{3}} \cdot (1+x^{5})-e^{x^{3}} \cdot (1+x^{5})'}{(1+x^{5})^{2}};$

Производная суммы равна сумме производных:

(u+v)'=u'+v';

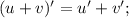
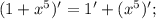
$(1+x^{5})'=1'+(x^{5})';$

1 — константа. Производная константы равна нулю.

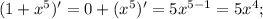
$(1+x^{5})'=0+(x^{5})'=5x^{5-1}=5x^{4};$

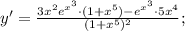
$y'=\frac{3x^{2}e^{x^{3}} \cdot (1+x^{5})-e^{x^{3}} \cdot 5x^{4}}{(1+x^{5})^{2}};$

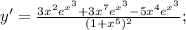
$y'=\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{(1+x^{5})^{2}};$

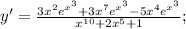
$y'=\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{x^{10}+2x^{5}+1};$

4,7(55 оценок)

Ответ:

мядель

31.07.2021

1. Сложить два известных угла, результат вычесть из 180 градусов.

2. Вычесть известный угол из 90 градусов; сложить известный угол с 90, результат вычесть из 180 градусов.

3. 82

4. 98

5. Отрезок BH образует со стороной АС угол в 90 градусов.

6. Точка M разделит отрезок АС пополам.

7. Отрезок BE разделит угол В пополам.

8. Углы при основании равны; биссектриса, проведенная к основанию, является медианой и высотой

9. Касательная, проведенная к окружности, перпендикулярна радиусу, проведенному к точке касания; из любой точки, лежащей вне окружности, можно провести ровно две касательные к окружности; отрезок, соединяющий точку, лежащую вне окружности, с центром окружности, является биссектрисой угла между касательными, проведенными из этой точки к окружности; отрезки касательных (к одной окружности!), проведенных из одной точки, равны.

10. Медианы делятся в отношении 2:1 считая от вершин треугольника.

4,7(23 оценок)

Это интересно:

Компьютеры-и-электроника

09.12.2022

Как взломать Wi-Fi сеть (WEP) с помощью Airoway и Wifislax...

Образование-и-коммуникации

08.01.2020

Как стать интересным: советы и рекомендации...

Образование-и-коммуникации

28.08.2021

Как написать описательный абзац: эффективные советы и примеры...