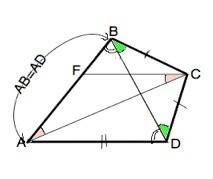
Проведем в данном четырехугольнике диагональ BD.
По услоию AF=FC, BC=CD, AB=AD ⇒
∆ АВD и ∆ ВСD - равнобедренные.
Рассмотрим треугольники АВС и АDС. Они равны по трем сторонам ( две по условию, сторона АС - общая)
Следовательно, ∠ВАС=∠DАС, ⇒ АС - биссектриса угла ВАD
В ∆ АFC стороны AF=CF, ∆ AFC – равнобедренный, ⇒ ∠FAC=∠FCA.
Но ∠ВАС=∠САD (из доказанного равенства ∆ АВС и ∆ АDС).
Из этого следует ∠FCA=∠CAD, а эти углы - накрестлежащие при пересечении FC и AD секущей АС.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти прямые параллельны. ⇒
FC||AD. Доказано.
1
Объяснение:
Пусть щупалец х, тогда ног от 0.33х до 0.42х, при этом число ног натуральное число.
Для х=100 минимальным будет 33 (наименьшее целое от 0.33*100=33 до 0.42*100=42). Попробуем найти меньшее.
Возьмем х=25. при процентном соотношении 0.36 (0.33<04.<0.42) ног будет от 0.33*25=8.25 до 0.42*25=10.5 -- наименьшее целое 9 при процентном соотношении 36% (25*36:100=9). Попробуем найти меньшее.
Возьмем х=5. Тогда ног будет от 0.33*5=1.65 до 0.42*5=2.1
При процентном соотношении 40% или же 0.4 ног будет 2. (5*40:100=2).
Теперь вопрос может ли быть лишь 1 нога.
При х=4 ног будет от 0.33*4=1.32 до 0.42*4=1.68 -- не подходит - нет целого числа между 1.32 и 1.68
При х =3 ног будет от 0.33*3=0.99 до 0.42*3=1.26. имеем что 1 входит в диапазон от 0.99 до 1.26. При этом процентное содержание будет выражаться в виде бесконечной десятичной дроби 0.(3) = 0.3333...
(если же речь идет о целом числе процентов то тогда возвращаемся к 2 ногам)
x^2-2x-4=0
x1,2=(2+-D)/2*1
D=√(2²-4*1*-4)=√(4+16)=√20=√(4*5)=2√5
x1,2=(2+-2√5)/2
x1=(2+2√5)/2=2*(1+√5)/2=1+√5
х2=(2-2√5)/2=2*(1-√5)/2=1-√5
Сумма квадратов корней данного квадратного уравнения :
(1+√5)²+(1-√5)²=1+2√5+5+1-2√5+5=12
ответ: Сумма квадратов корней равна 12