Алгебра: А) (y-4) в квадрате. б) (7x+a) в квадрате- преобразуйте многочлен

А) (y-4) в квадрате. б) (7x+a) в квадрате- преобразуйте многочлен

👇

Увидеть ответ

Ответ:

danabekzanova

09.06.2023

А)(у-4)²=у²-8у+16 б)(7х+а)²=49х²+14ха+а²

4,7(35 оценок)

Открыть все ответы

Ответ:

serofimtimoxa

09.06.2023

Следует отметить, что когда вычисляется частная производная от функции многих переменных по некоторой переменной, то остальные переменные рассматриваются как константы.

1) Дана сложная функция двух переменных

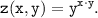
$\displaystyle \tt z(x, y)=y^{x \cdot y}.$

Область определения функции: y>0, y≠1.

Находим частные производные.

Так как переменная х участвует только в показателе функции z(x, y), то частную производную по х находим как от показательной функции с основанием y, в показателе которой сложная функция:

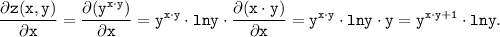
$\displaystyle \tt \frac{ \partial z(x,y)}{ \partial x} = \frac{ \partial (y^{x \cdot y})}{ \partial x} = y^{x \cdot y} \cdot lny \cdot \frac{ \partial (x \cdot y)}{ \partial x} = y^{x \cdot y} \cdot lny \cdot y = y^{x \cdot y+1} \cdot lny.$

ответ: 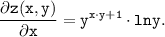$\displaystyle \tt \frac{ \partial z(x,y)}{ \partial x} = y^{x \cdot y+1} \cdot lny.$

Для нахождения частную производную по у поступим следующим образом.

а) Логарифмируем по основанию e обе стороны выражения 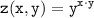$\displaystyle \tt z(x, y)=y^{x \cdot y}$ :

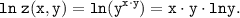
$\displaystyle \tt ln \; z(x, y)=ln (y^{x \cdot y})=x \cdot y \cdot lny.$

б) Находим частную производную по у от левой части последнего выражения:

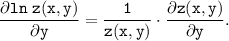
$\displaystyle \tt \frac{ \partial ln \; z(x,y)}{ \partial y} = \frac{1}{z(x,y)} \cdot \frac{ \partial z(x,y)}{ \partial y}.$

Находим частную производную по у от правой части последнего выражения как производная от произведения:

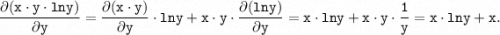
$\displaystyle \tt \frac{ \partial (x \cdot y \cdot lny)}{ \partial y} = \frac{ \partial (x \cdot y)}{ \partial y} \cdot lny+x \cdot y \cdot \frac{ \partial (lny)}{ \partial y}=x \cdot lny + x \cdot y \cdot \frac{1}{y} =x \cdot lny + x.$

в) Имеем:

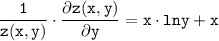
$\displaystyle \tt \frac{1}{z(x,y)} \cdot \frac{ \partial z(x,y)}{ \partial y} =x \cdot lny + x$

или

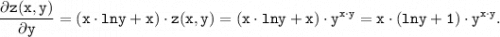
$\displaystyle \tt \frac{ \partial z(x,y)}{ \partial y} =(x \cdot lny + x) \cdot z(x,y)=(x \cdot lny + x) \cdot y^{x \cdot y}=x \cdot (lny + 1) \cdot y^{x \cdot y}.$

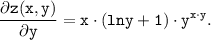
ответ: $\displaystyle \tt \frac{ \partial z(x,y)}{ \partial y} =x \cdot (lny + 1) \cdot y^{x \cdot y}.$

2) Дана сложная функция двух переменных

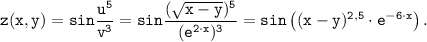
$\displaystyle \tt z(x, y)=sin\frac{u^5}{v^3} = sin\frac{(\sqrt{x-y} )^5}{(e^{2 \cdot x})^3}=sin\left ((x-y )^{2,5} \cdot e^{-6 \cdot x} \right ).$

Область определения функции: x-y≥0.

Находим частные производные как от сложной функции.

Частная производная по х:

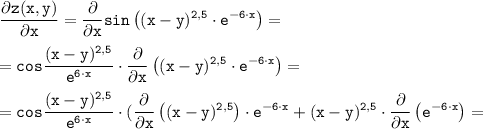
$\displaystyle \tt \frac{ \partial z(x,y)}{ \partial x} = \frac{ \partial }{ \partial x} sin\left ((x-y )^{2,5} \cdot e^{-6 \cdot x} \right )= \\\\=cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot \frac{ \partial }{ \partial x} \left ((x-y )^{2,5} \cdot e^{-6 \cdot x} \right ) = \\\\= cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot (\frac{ \partial }{ \partial x} \left ((x-y )^{2,5} \right ) \cdot e^{-6 \cdot x} + (x-y )^{2,5} \cdot \frac{ \partial }{ \partial x} \left (e^{-6 \cdot x} \right ) \right )=$

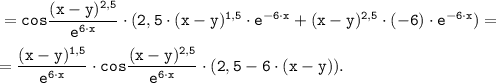
$\displaystyle \tt = cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot (2,5 \cdot (x-y)^{1,5} \cdot e^{-6 \cdot x} + (x-y )^{2,5} \cdot (-6) \cdot e^{-6 \cdot x} ) =\\\\= \frac{(x-y )^{1,5}}{e^{6 \cdot x}} \cdot cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot (2,5-6\cdot (x-y)).$

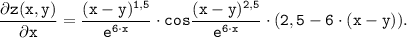
ответ: $\displaystyle \tt \displaystyle \tt \frac{ \partial z(x,y)}{ \partial x} = \frac{(x-y )^{1,5}}{e^{6 \cdot x}} \cdot cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot (2,5-6\cdot (x-y)).$

Частная производная по у:

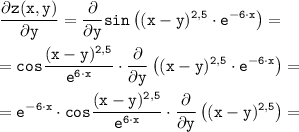
$\displaystyle \tt \frac{ \partial z(x,y)}{ \partial y} = \frac{ \partial }{ \partial y} sin\left ((x-y )^{2,5} \cdot e^{-6 \cdot x} \right )= \\\\= cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot \frac{ \partial }{ \partial y} \left ((x-y )^{2,5} \cdot e^{-6 \cdot x} \right ) = \\\\=e^{-6 \cdot x} \cdot cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot \frac{ \partial }{ \partial y} \left ((x-y )^{2,5} \right ) =$

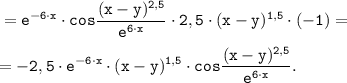
$\displaystyle \tt =e^{-6 \cdot x} \cdot cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} \cdot 2,5 \cdot (x-y )^{1,5} \cdot (-1)=\\\\=-2,5 \cdot e^{-6 \cdot x} \cdot(x-y )^{1,5} \cdot cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} .$

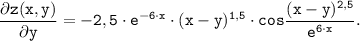
ответ: $\displaystyle \tt \frac{ \partial z(x,y)}{ \partial y} =-2,5 \cdot e^{-6 \cdot x} \cdot(x-y )^{1,5} \cdot cos\frac{(x-y )^{2,5}}{e^{6 \cdot x}} .$