1. Функция y=x²-6x+3 представляет собой параболу. Чтобы построить ее график, мы можем использовать несколько способов.
Способ 1: Используя формулу для нахождения вершины параболы.
Функция имеет общий вид y=ax²+bx+c. Если коэффициент a положительный, парабола открывается вверх, а если отрицательный - вниз. В нашей функции a=1, что означает, что парабола будет направлена вверх.
Для нахождения координат вершины параболы можно использовать формулы:
x_вершины = -b/(2a)
y_вершины = f(x_вершины)
Подставляя значения a=1, b=-6 и c=3 в формулы:
x_вершины = -(-6)/(2*1) = 6/2 = 3
y_вершины = 3²-6*3+3 = 9-18+3 = -6
Таким образом, координаты вершины параболы равны (3, -6).
Способ 2: С помощью построения таблицы значений и построения графика.
Для построения таблицы значений замените x на несколько разных значений и вычислите соответствующие значения y.
Постройте график, используя полученные значения и нарисуйте плавную кривую, проходящую через эти точки. Значение y будет на вершине параболы.
2. Для нахождения области значений функции y=-x²-8x+1 мы можем использовать методы графика или анализа дискриминанта.
Способ 1: Графический метод. Построим график функции y=-x²-8x+1, используя таблицу значений или рисуя кривую, проходящую через несколько точек. Область, которую занимают значения y, будет областью значений нашей функции.
Способ 2: Анализ дискриминанта. Для определения области значений, рассмотрим общую формулу функции параболы: y=ax²+bx+c. Если коэффициент a положительный, то парабола направлена вверх и ее значение возрастает с удалением от вершины. Если a отрицательное, то парабола направлена вниз и ее значение убывает.
У нас заданная функция y=-x²-8x+1 имеет a=-1, что означает, что парабола направлена вниз и ее значение убывает. Это означает, что область значений функции - это все отрицательные числа и числа, большие или равные значению функции в вершине параболы.
Для нахождения вершины параболы, мы можем использовать формулы:
x_вершины = -b/(2a)
y_вершины = f(x_вершины)
Подставляем значения a=-1 и b=-8 в формулу:
x_вершины = -(-8)/(2*(-1)) = 8/(-2) = -4
y_вершины = -(-4)²-8*(-4)+1 = -16+32+1 = 17
Таким образом, координаты вершины параболы равны (-4, 17).
Исходя из этого, можно сказать, что область значений функции y=-x²-8x+1 будет вся вещественная ось y, начиная с значения в вершине параболы и убывающая до бесконечности.
3. Чтобы найти координаты точек пересечения параболы y= ¼x² и прямой y=5x-16, мы должны найти значения x, которые удовлетворяют обоим уравнениям.
Подставим уравнение прямой вместо y в уравнение параболы:
¼x² = 5x - 16
Умножим оба выражения на 4, чтобы избавиться от дробей:
x² = 20x - 64
Теперь перенесем все выражения в одну сторону и получим квадратное уравнение:
x² - 20x + 64 = 0
Факторизуем это уравнение или используем квадратное уравнение для нахождения корней. Поскольку это предмет школьной программы, то для нашего уровня будем использовать факторизацию:
(x - 4)(x - 16) = 0
Из этого уравнения получаем два значения x:
x₁ = 4
x₂ = 16
Теперь мы можем подставить эти значения x в одно из уравнений, чтобы найти соответствующие значения y.
Для x = 4:
y = ¼(4)² = ½
Для x = 16:
y = ¼(16)² = 16
Таким образом, точки пересечения параболы и прямой являются (4, ½) и (16, 16).
4. Чтобы найти значение a и построить график функции y=-x²+ax+3, если известно, что он проходит через точку (2,-5):
Подставим значения x и y в уравнение:
-5 = -(2)² + 2a + 3
а) Так как 0° < α < 90° - первая четверть, то в первой четверти синус положителен. Из основного тригонометрического тождества
sin²α + cos²α = 1
Найдем sinα: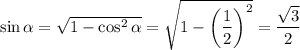
б) Так как π < α < 3π/2 - третья четверть, то в третьей четверти косинус отрицателен, находим косинус из основного тригонометрического тождества: