Абсолютной величиной (или абсолютным значением) отрицательного числаназывается положительное число, получаемое от перемены его знака (-) на обратный (+). Абсолютная величина -5 есть +5, т. е. 5. Абсолютной величиной положительного числа (а также числа 0) называется само это число.
Знак абсолютной величины - две прямые черты, в которые заключается число, абсолютная величина которого берется. Например,
|-5| = 5,
|+5| = 5,
| 0 | = 0.
Примеры.
(+8) + (+11) = 19;
(-7) + (-3) = -10.
б) При сложении двух чисел с разными знаками из абсолютной величины одного из них вычитается абсолютная величина другого (меньшая из большей) а ставится знак того числа, у которого абсолютная величина больше.
Примеры.
(-3) + (+12) = 9;
(-3) + (+1) = -2.
Примеры.
(+7) - (+4) = (+7) + (-4) = 3;
(+7) - (-4) = (+7) + (+4) = 11;
(-7) - (-4) = (-7) + (+4) = -3;
(-4) - (-4) = (-4) + (+4) = 0;
Замечание. При выполнении сложения и вычитания, особенно когда имеем дело с несколькими числами, лучше всего поступать так:
1) освободить все числа от скобок, при этом перед числом поставить знак «+ », если прежний знак перед скобкой был одинаков со знаком в скобке, и « -», если он был противоположен знаку в скобке;
2) сложить абсолютные величины всех чисел, имеющих теперь слева знак +;
3) сложить абсолютные величины всех чисел, имеющих теперь слева знак -;
4) из большей суммы вычесть меньшую и поставить знак, соответствующий большей сумме.
Пример.
(-30) - (-17) + (-6) - (+12) + (+2);
(-30) - (-17) + (-6) - (+12) + (+2) = -30 + 17 - 6 - 12 + 2;
17 + 2 = 19;
30 + 6 + 12 = 48;
48 - 19 = 29.
Результат есть отрицательное число -29, так как большая сумма (48) получилась от сложения абсолютных величин тех чисел, перед которыми стоили минусы в выражении -30 + 17 – 6 -12 + 2. На это последнее выражение можно смотреть и как на сумму чисел -30, +17, -6, -12, +2, и как на результат последовательного прибавления к числу -30 числа 17, затем вычитания числа 6, затем вычитания 12и, наконец, прибавления 2. Вообще на выражение а - b + с - d и т. д. можно смотреть и как на сумму чисел (+а), (-b), (+с), (-d), и как на результат таких последовательных действий: вычитания из (+а) числа (+b) , прибавления ( +c), вычитании ( +d) и т. д.
Схема (правило знаков при умножении):
Примеры.
(+1/3) * (+2) * (-6) * (-7) * (-1/2) = 7 (три отрицательных сомножителя);
(-1/3) * (+2) * (-3) * (+7) * (+1/2) = 7 (два отрицательных сомножителя).
Примеры.
(-6) : (+3) = -2;
(+8) : (-2) = -4;
(-12) : (-12) = + 1
Задание 1. Решить уравнения.
а) 1,2(x - 3) + 0,4(1 - x) = 4
1,2x - 3,6 + 0,4 - 0,4x = 4
1,2x - 0,4x = 4 + 3,6 - 0,4
0,8x = 7,2
x = 7,2 : 0,8 = 9
ответ: 9
б) Здесь, очевидно, что в числителях забыли скобки:
(2 - 3x)/4 + (1 - x)/2 = (4 - 3x)/8
Умножим всё уравнение на 8
2(2 - 3x) + 4(1 - x) = 4 - 3x
4 - 6x + 4 - 4x = 4 - 3x
4 + 4 - 4 = 6x + 4x - 3x
7x = 4
x = 4/7
ответ: 4/7
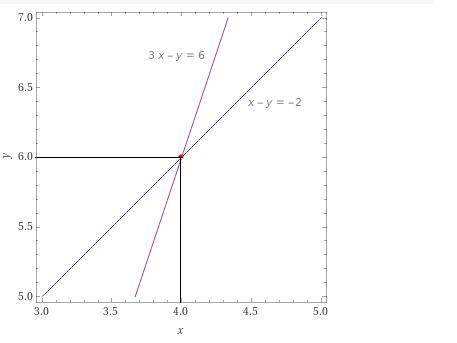
Задание 2. Определить количество решений системы графическим методом. Записать алгоритм построения графиков.
Здесь надо построить графики и найти, где они пересекаются.
{ x - y = -2
{ 3x - y = 6
Выразим игреки через иксы:
{ y = x + 2
{ y = 3x - 6
Они пересекутся в точке (4; 6).
ответ: Решение единственное и оно показано на рисунке.
Задание 3. Решить систему уравнений.
Здесь, очевидно, в числителях опять забыли скобки, как в 1. б):
{ (x + 4)/5 - (y - 1)/8 = 1
{ (x + 2)/9 - (y - 3)/6 = 2/3
Умножаем 1 уравнение на 40, а 2 уравнение на 18:
{ 8(x + 4) - 5(y - 1) = 40
{ 2(x + 2) - 3(y - 3) = 12
Раскрываем скобки:
{ 8x + 32 - 5y + 5 = 40
{ 2x + 4 - 3y + 9 = 12
Приводим подобные:
{ 8x - 5y = 40 - 32 - 5 = 3
{ 2x - 3y = 12 - 4 - 9 = -1
Умножаем 2 уравнение на -4:
{ 8x - 5y = 3
{ -8x + 12y = 4
И складываем уравнения:
8x - 5y - 8x + 12y = 3 + 4
7y = 7
y = 1
8x = 3 + 5y = 3 + 5*1 = 6
x = 1
ответ: (1; 1)
Задание 4. Составить математическую модель задачи и решить её.
Один сплав мед и цинка имеет массу m1 кг и содержит 8% цинка.
Второй сплав имеет массу m2 кг и содержит 24% цинка.
Вместе они дают сплав массой 300 кг, содержащий 12% цинка.
Найти массы начальных сплавов m1 и m2.
Во-первых, можно найти, что m2 = 300 - m1.
Во-вторых, сплавы содержат 0,08*m1 кг и 0,24(300-m1) кг цинка.
Конечный сплав содержит 300*0,12 = 36 кг цинка.
Математическая модель задачи - это уравнение:
0,08*m1 + 0,24(300 - m1) = 36
Решаем его. Раскрываем скобки:
0,08*m1 + 72 - 0,24*m1 = 36
72 - 36 = 0,24*m1 - 0,08*m1
0,16*m1 = 36
m1 = 36/0,16 = 3600/16 = 900/4 = 225 кг - масса 1 сплава.
m2 = 300 - m1 = 300 - 225 = 75 кг = масса 2 сплава.
ответ: 225 кг сплава 8% и 75 кг сплава 24%.
f(x)= -7*3x^2 + 10*2x +1=-21x^2+20x+1