квадрат любого числа не может быть с минусом, и у примера нет решений. Когда мы возносим любое число ( даже отрицательное) мы его умножаем само на себя, и если с натуральными числами все понятно, то с отрицательными мы умножая - ( отрицательное число) на - ( отрицательное число) получаем + ( положительное число), и даже если мы умножаем одно и тоже число на себя четное количество раз, у нас в ответе будет +, а если нечётное то -, а квадрат подразумевает что мы умножаем число два раза ( двойка четное число) и естественно - в ответе не может быть. Из этого делаем вывод что -х² не имеет значения ∅, и естественно что весь пример не имеет решения
1. Табличка во вложении:
4Гб - апрель
1Гб - июль
3Гб - июнь
5Гб - нет
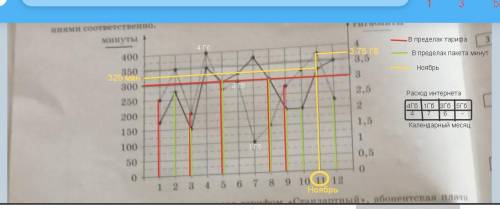
2. Расходы за ноябрь (11месяц):
Стоимость услуги связи = 400 руб.,
Превышение лимита минут:
лимит - 300 мин., израсходовано - 325 мин.
цена минуты сверх лимита - 2.5 р/мин.,
325-300=25 мин. сверх лимита;
25*2.5=62.5 руб. - за превышение лимита минут.
Превышение пакета инета:
Пакет = 3Гб;
Израсходовано - 3.75ГБ;
3.75-3=0.75Гб сверх лимита.
Превышение лимита по инету - 0.5Гб=80 руб.,
0.75*80=120 руб. за превышение лимита инетаю
Всего: 400+62.5+120=582.5 руб. оплачено за ноябрь
3. Не превышал лимит по пакету минут: 7 мес.
4. Не превышал лимит по пакетам минут и инета: 5 мес.
График во вложении
1) первая скобка стоит во 2-й степени, значит её значение ≥ 0
2) наше неравенство строгое, значит, надо убрать число, которое превращает в нуль первую скобку.
х + 1 - √3 = 0
х = √3 -1
3) результат в примере > 0, значит, вторая скобка должна быть > 0.
x - √6 + 2 > 0
x > √6 - 2
4) -∞ √6 +2 +∞
Теперь надо выяснить, где находится число √3 - 1
(√3 - 1 - √6 - 2 = √3 - √6 - 3 <0, ⇒ √3 - 1 > √6 + 2, значит число
√3 - 1 стоит правее , чем число √6 + 2)
ответ: х∈(√6 + 2; √3 -1) ∪(√3 - 1 ; +∞)