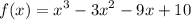
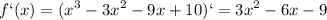
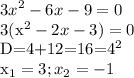
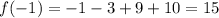
Ну, первым делом было бы неплохо вычислить длины векторов a=3m+2n и b=-m+3n. Это можно сделать примерно так:
|a|^2 = <a,a> = <3m+2n,3m+2n> =
<3m, 3m> + 2<2n, 3m> + <2n, 2n> =
9|m|^2 + 12<m, n> + 4|n|^2
|b|^2 = <b,b> = <-m+3n,-m+3n> =
<-m, -m> - 2<m,3n> + <3n, 3n> =
|m|^2 - 6<m, n> + 9|n|^2
Угол между a и b будет вычисляться примерно так:
cos(ab) = <a,b> / (|a| * |b|)
Скалярное произведение имеет вид:
<a,b> = <3m+2n,-m+3n> =
<3m,-m> + <2n,-m> + <3m,3n> + <2n,3n> =
-3|m|^2 - 2 <n,m> + 9<m,n> + 4|n|^2 =
-3|m|^2 + 7 <n,m> + 4|n|^2
Получили выражение косинуса через известные величины. До числа, думаю, доведёте сами. 8-)
раскрываем скобки в правой части уравнения:
x^2+11x+24=x^2-ax+8x-8a
видя "ax" начинаем плакать, но не сдаемся, переносим некоторые числа в правую часть:
x^2-x^2+11x-8x+ax=-8a-24
решаем:
3x+ax=-8a-24
хммм.. что тут можно сделать? попробуем вынести за скобки некоторые коэффициенты в правой и в левой части:
x(a+3)=-8(a+3)
видим, что две скобки одинаковы "(a+3)", пробуем сократить:
x(a+3)=-8(a+3) |:(a+3) x≠-3(пишем на всякий вот это т.к сокращаем)
сокращаем:
x=-8
ура ответ! наверно, правильный ! (нет)
ответ: x=-8