Яне было в этом теме . поэтому не понела . знаю что много ,но зделайте хоть что нибудь . завтра сдавать 1. выражение: а) (х - 3) (х - 7) - 2х (3х - 5); б) 4а (а - 2) - (а - 4)2; в) 2 (т + 1)2 - 4m. • 2. разложите на множители: а) х3 - 9х; б) -5а2 - 10аb - 5b2. 3. выражение (у2 - 2у)2 - у2(у + 3) (у - 3) + 2у (2у2 + 5). 4. разложите на множители: а) 16х4 - 81; б) х2 - х - у2 - у. 5. докажите, что выражение х2 - 4х + 9, при любых значениях х принимает положительные значения.

👇

Ответ:

ivkov2003

07.05.2022

1) Раскрываем скобки. Перемножаем каждое число на каждое.
а) (x - 3)(x - 7) - 2x(3x - 5) = x*x - 3*x - 7*x - 3(-7) - 2x*3x - 2x(-5) =
= x^2 - 10x + 21 - 6x^2 + 10x = -5x^2 + 21
б) 4a(a - 2) - (a - 4)^2 = 4a^2 - 8a - (a^2 - 8a + 16) =
= 4a^2 - 8a - a^2 + 8a - 16 = 3a^2 - 16
в) 2(m+1)^2 - 4m = 2(m^2+2m+1) - 4m = 2m^2 + 4m + 2 - 4m = 2m^2 + 2

2) а) Выносим х за скобки и раскладываем разность квадратов
x^3 - 9x = x(x^2 - 9) = x(x - 3)(x + 3)
б) Выносим -5 за скобки и получаем квадрат суммы
-5a^2 - 10ab - 5b^2 = -5(a^2 + 2ab + b^2) = -5(a + b)^2

3) Раскрываем скобки
(y^2 - 2y)^2 - y^2(y + 3)(y - 3) + 2y(2y^2 + 5) =
= y^4 - 4y^3 + 4y^2 - y^2(y^2 - 9) + 4y^3 + 10y =
= y^4 - 4y^3 + 4y^2 - y^4 + 9y^2 + 4y^3 + 10y = 13y^2 + 10y

4) а) Разность квадратов два раза
16x^4 - 81 = (4x^2 - 9)(4x^2 + 9) = (2x - 3)(2x + 3)(4x^2 + 9)
б) Разность квадратов
x^2 - x - y^2 - y = (x^2 - y^2) - (x + y) = (x-y)(x+y) - (x+y) = (x+y)(x-y-1)

5) x^2 - 4x + 9 = x^2 - 4x + 4 + 5 = (x - 2)^2 + 5
При любом х значение квадрата >= 0, а выражения >= 5

4,4(11 оценок)

Открыть все ответы

Ответ:

приветпока4

07.05.2022

1) Общее количество получить 5 вопросов из 50:

C(50,5) = 50! / (5! · (50 - 5)!) = 46 · 47 · 48 · 49 · 50 / (1 · 2 · 3 · 4 · 5) = 2118760;

Количество получить 4 вопроса из 30, которые студент знает:

C(30,4) = 30! / (4! · (30 - 4)!) = 27 · 28 · 29 · 30 / (1 · 2 · 3 · 4) = 27405;

Количество получить один вопрос из 20, которые студент не знает:

C(20,1) = 20.

Вероятность того, что студент ответит на 4 вопроса из 5:

P = C(30,4) · C(20,1) / C(50,5) = 27405 · 1 / 2118760 = 0,259.

2) Вероятность того, что студент ответит на вопрос: p = 30/50 = 3/5;

Вероятность того, что студент не ответит на вопрос: q = 1 - p = 1 - 3/5 = 2/5;

Наивероятнейшее число правильных ответов будем искать по формуле:

np − q ≤ k ≤ np + p; где n = 5 - число вопросов, k - наивероятнейшее число правильных ответов.

5 · 3/5 - 2/5 ≤ k ≤ 5 · 3/5 + 3/5;

3 - 0,4 ≤ k ≤ 3 + 0,6;

2,6 ≤ k ≤ 3,6;

k = 3; (k должно быть целым числом).

ответ: Вероятность ответить на 4 вопроса 0,259; наивероятнейшее число правильных ответов: k = 3.

4,6(71 оценок)

Ответ:

kazybekabdrahman0707

07.05.2022

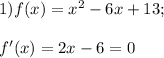
$1) f(x)=x^2-6x+13;\\\\f'(x)=2x-6=0\\\\$

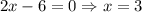$2x-6=0\Rightarrow x=3$ - критическая точка.

Для нахождение наименьшего и наибольшего значения на отрезке найдем значение функции в критической точке и на концах отрезка - при x = 0, x = 3 и x = 6.

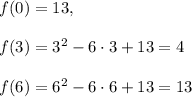
$f(0) = 13,\\\\f(3) = 3^2-6\cdot3+13=4\\\\f(6)=6^2-6\cdot6+13=13$

$\max_{[0; 6]}f(x)=f(0)=f(6)=13.\\\min_{[0; 6]}f(x)=f(3)=4.$

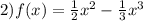
$2) f(x)=\frac{1}{2}x^2- \frac{1}{3}x^3$

$f'(x)=x-x^2=0\\\\$

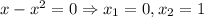$x-x^2=0\Rightarrow x_1=0, x_2=1$ - критические точки.

Первая точка в заданный промежуток не попадает, а вторая совпадает с левым ее концом, поэтому для нахождение наименьшего и наибольшего значения на отрезке достаточно найти значение функции на концах отрезка: при х = 1 и х = 3.

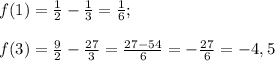
$f(1)=\frac{1}{2}-\frac{1}{3}=\frac{1}{6};\\\\ f(3)=\frac{9}{2}-\frac{27}{3}=\frac{27-54}{6}=-\frac{27}{6}=-4,5$

$\max_{[1; 3]}f(x)=f(1)=1/6.\\\min_{[1; 3]}f(x)=f(3)=-4,5.$

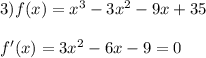
$3) f(x) = x^3-3x^2-9x+35\\\\f'(x)=3x^2-6x-9=0\\$

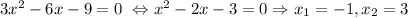$3x^2-6x-9=0\ \Leftrightarrow x^2-2x-3=0\Rightarrow x_1=-1, x_2=3$ - критические функции.

Для нахождение наименьшего и наибольшего значения на отрезке найдем значение функции в критических точках и на концах отрезка - при x = -4, x = -1, x = 3 и х = 4:

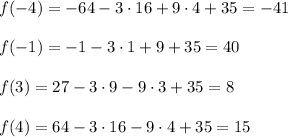
$f(-4)=-64-3\cdot16+9\cdot4+35=-41\\\\f(-1)=-1-3\cdot1+9+35=40\\\\f(3)=27-3\cdot9-9\cdot3+35=8\\\\f(4)=64-3\cdot16-9\cdot4+35=15$