Объяснение:
эти уравнения решаются совсем не сложно,особенно если можешь приводить дроби к общему знаменателю и решать простые уравнения.
Т.к в знаменателе этих уравнений стоят натуральные числа,то мы можем "избавиться "от этих знаменателей,для этого надо найти их общий знаменатель и после умножения сократить.
решение двух примеров внизу.все остальные решаются аналогично.попробуй решить самостоятельно,смотри на мое решение.вся сложность заключается в нахождении общего знаменателя.,для этого надо найти НОК старых знаменателей.
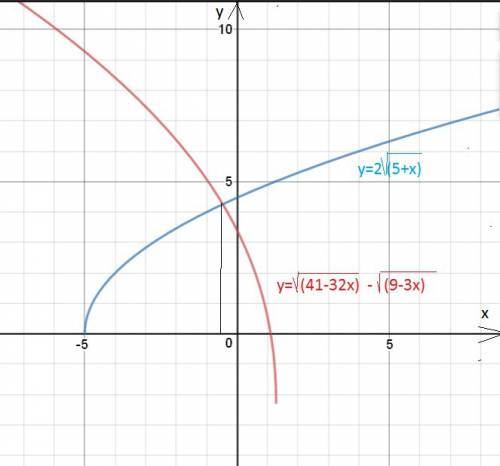
41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
2.txč.
dve3č.50min.= (3+5/6)č. = 23/6č.
1č. 1.t. 1/7
2.t. 1/x
dve6/23
1/7+1/x=6/23 /.23.7.x
23x+161=42x
19x=161,x=161/19,x=(8+9/19)č.